Robust High-dimensional Tuning Free Multiple Testing
Paper and Code
Nov 23, 2022
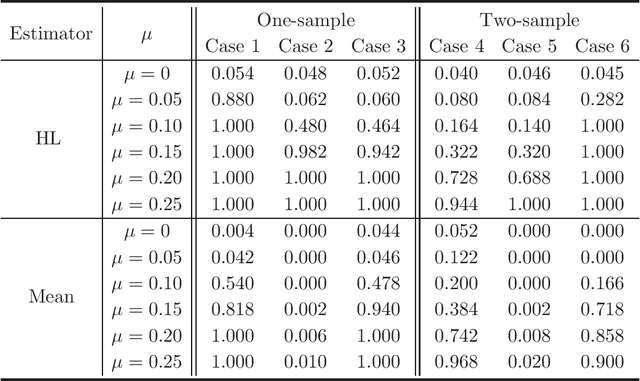
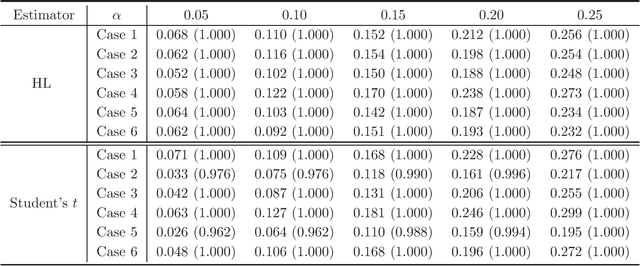
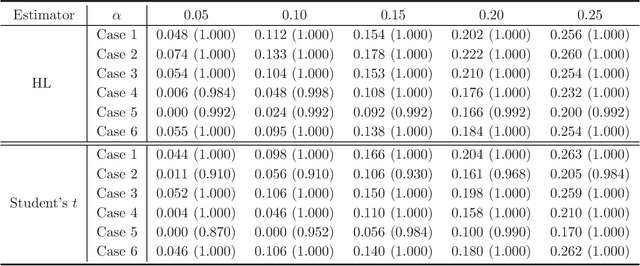
A stylized feature of high-dimensional data is that many variables have heavy tails, and robust statistical inference is critical for valid large-scale statistical inference. Yet, the existing developments such as Winsorization, Huberization and median of means require the bounded second moments and involve variable-dependent tuning parameters, which hamper their fidelity in applications to large-scale problems. To liberate these constraints, this paper revisits the celebrated Hodges-Lehmann (HL) estimator for estimating location parameters in both the one- and two-sample problems, from a non-asymptotic perspective. Our study develops Berry-Esseen inequality and Cram\'{e}r type moderate deviation for the HL estimator based on newly developed non-asymptotic Bahadur representation, and builds data-driven confidence intervals via a weighted bootstrap approach. These results allow us to extend the HL estimator to large-scale studies and propose \emph{tuning-free} and \emph{moment-free} high-dimensional inference procedures for testing global null and for large-scale multiple testing with false discovery proportion control. It is convincingly shown that the resulting tuning-free and moment-free methods control false discovery proportion at a prescribed level. The simulation studies lend further support to our developed theory.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge