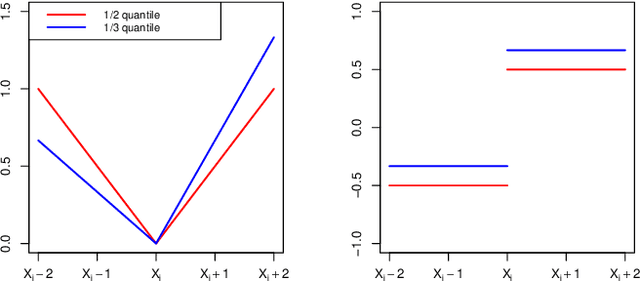
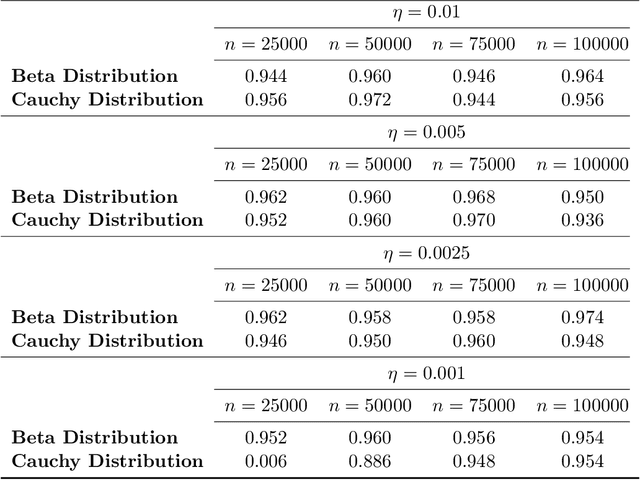
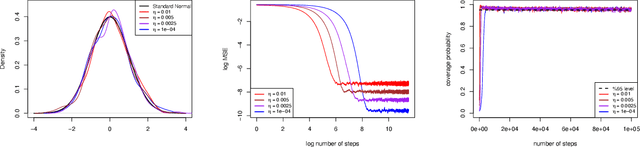
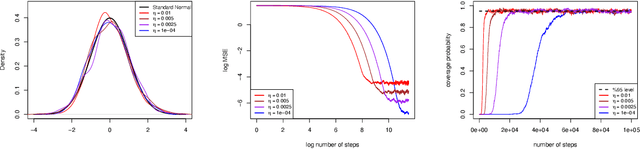
Online Inference for Quantiles by Constant Learning-Rate Stochastic Gradient Descent

This paper proposes an online inference method of the stochastic gradient descent (SGD) with a constant learning rate for quantile loss functions with theoretical guarantees. Since the quantile loss function is neither smooth nor strongly convex, we view such SGD iterates as an irreducible and positive recurrent Markov chain. By leveraging this interpretation, we show the existence of a unique asymptotic stationary distribution, regardless of the arbitrarily fixed initialization. To characterize the exact form of this limiting distribution, we derive bounds for its moment generating function and tail probabilities, controlling over the first and second moments of SGD iterates. By these techniques, we prove that the stationary distribution converges to a Gaussian distribution as the constant learning rate $\eta\rightarrow0$. Our findings provide the first central limit theorem (CLT)-type theoretical guarantees for the last iterate of constant learning-rate SGD in non-smooth and non-strongly convex settings. We further propose a recursive algorithm to construct confidence intervals of SGD iterates in an online manner. Numerical studies demonstrate strong finite-sample performance of our proposed quantile estimator and inference method. The theoretical tools in this study are of independent interest to investigate general transition kernels in Markov chains.

Detecting Backdoor Attacks via Similarity in Semantic Communication Systems

Semantic communication systems, which leverage Generative AI (GAI) to transmit semantic meaning rather than raw data, are poised to revolutionize modern communications. However, they are vulnerable to backdoor attacks, a type of poisoning manipulation that embeds malicious triggers into training datasets. As a result, Backdoor attacks mislead the inference for poisoned samples while clean samples remain unaffected. The existing defenses may alter the model structure (such as neuron pruning that potentially degrades inference performance on clean inputs, or impose strict requirements on data formats (such as ``Semantic Shield" that requires image-text pairs). To address these limitations, this work proposes a defense mechanism that leverages semantic similarity to detect backdoor attacks without modifying the model structure or imposing data format constraints. By analyzing deviations in semantic feature space and establishing a threshold-based detection framework, the proposed approach effectively identifies poisoned samples. The experimental results demonstrate high detection accuracy and recall across varying poisoning ratios, underlining the significant effectiveness of our proposed solution.

High Confidence Level Inference is Almost Free using Parallel Stochastic Optimization

Uncertainty quantification for estimation through stochastic optimization solutions in an online setting has gained popularity recently. This paper introduces a novel inference method focused on constructing confidence intervals with efficient computation and fast convergence to the nominal level. Specifically, we propose to use a small number of independent multi-runs to acquire distribution information and construct a t-based confidence interval. Our method requires minimal additional computation and memory beyond the standard updating of estimates, making the inference process almost cost-free. We provide a rigorous theoretical guarantee for the confidence interval, demonstrating that the coverage is approximately exact with an explicit convergence rate and allowing for high confidence level inference. In particular, a new Gaussian approximation result is developed for the online estimators to characterize the coverage properties of our confidence intervals in terms of relative errors. Additionally, our method also allows for leveraging parallel computing to further accelerate calculations using multiple cores. It is easy to implement and can be integrated with existing stochastic algorithms without the need for complicated modifications.

Weighted Averaged Stochastic Gradient Descent: Asymptotic Normality and Optimality

Stochastic Gradient Descent (SGD) is one of the simplest and most popular algorithms in modern statistical and machine learning due to its computational and memory efficiency. Various averaging schemes have been proposed to accelerate the convergence of SGD in different settings. In this paper, we explore a general averaging scheme for SGD. Specifically, we establish the asymptotic normality of a broad range of weighted averaged SGD solutions and provide asymptotically valid online inference approaches. Furthermore, we propose an adaptive averaging scheme that exhibits both optimal statistical rate and favorable non-asymptotic convergence, drawing insights from the optimal weight for the linear model in terms of non-asymptotic mean squared error (MSE).