Communication-Efficient Distributed Estimation and Inference for Cox's Model

Motivated by multi-center biomedical studies that cannot share individual data due to privacy and ownership concerns, we develop communication-efficient iterative distributed algorithms for estimation and inference in the high-dimensional sparse Cox proportional hazards model. We demonstrate that our estimator, even with a relatively small number of iterations, achieves the same convergence rate as the ideal full-sample estimator under very mild conditions. To construct confidence intervals for linear combinations of high-dimensional hazard regression coefficients, we introduce a novel debiased method, establish central limit theorems, and provide consistent variance estimators that yield asymptotically valid distributed confidence intervals. In addition, we provide valid and powerful distributed hypothesis tests for any coordinate element based on a decorrelated score test. We allow time-dependent covariates as well as censored survival times. Extensive numerical experiments on both simulated and real data lend further support to our theory and demonstrate that our communication-efficient distributed estimators, confidence intervals, and hypothesis tests improve upon alternative methods.

Factor-Augmented Regularized Model for Hazard Regression

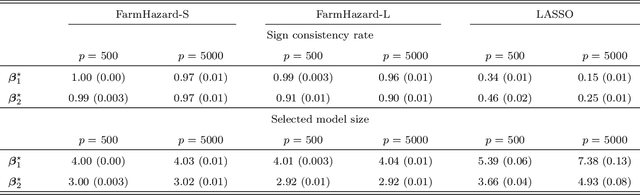
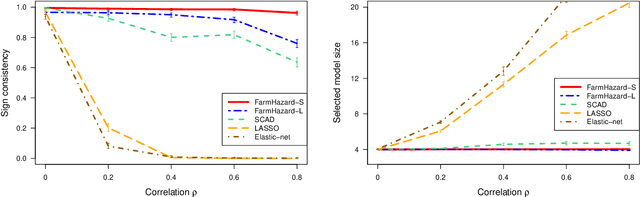
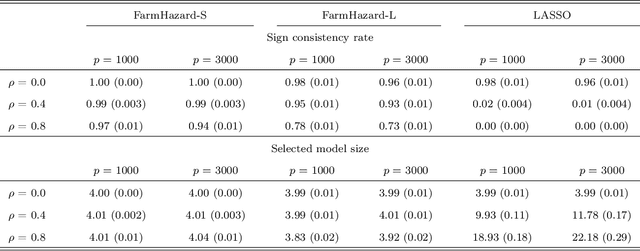
A prevalent feature of high-dimensional data is the dependence among covariates, and model selection is known to be challenging when covariates are highly correlated. To perform model selection for the high-dimensional Cox proportional hazards model in presence of correlated covariates with factor structure, we propose a new model, Factor-Augmented Regularized Model for Hazard Regression (FarmHazard), which builds upon latent factors that drive covariate dependence and extends Cox's model. This new model generates procedures that operate in two steps by learning factors and idiosyncratic components from high-dimensional covariate vectors and then using them as new predictors. Cox's model is a widely used semi-parametric model for survival analysis, where censored data and time-dependent covariates bring additional technical challenges. We prove model selection consistency and estimation consistency under mild conditions. We also develop a factor-augmented variable screening procedure to deal with strong correlations in ultra-high dimensional problems. Extensive simulations and real data experiments demonstrate that our procedures enjoy good performance and achieve better results on model selection, out-of-sample C-index and screening than alternative methods.

Cross-validation Confidence Intervals for Test Error

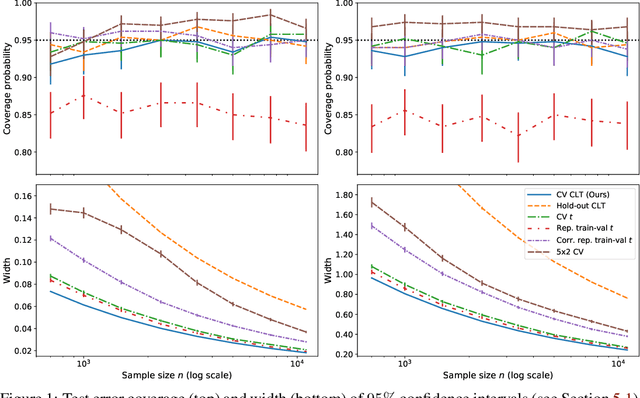
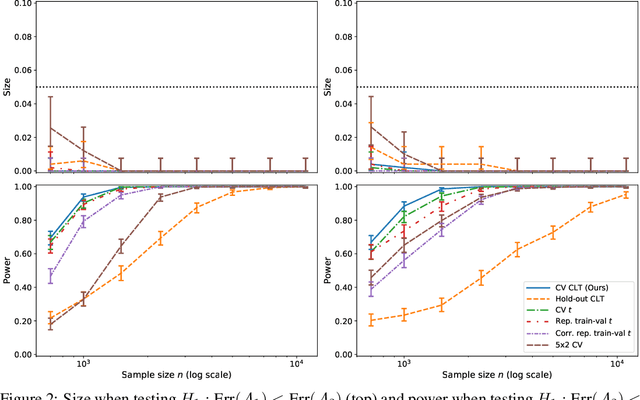
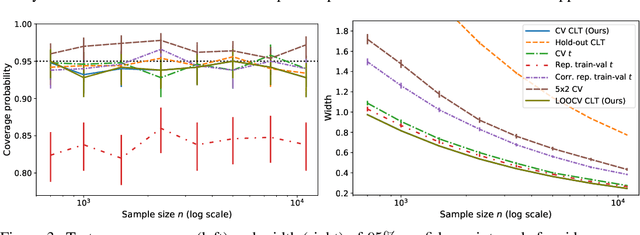
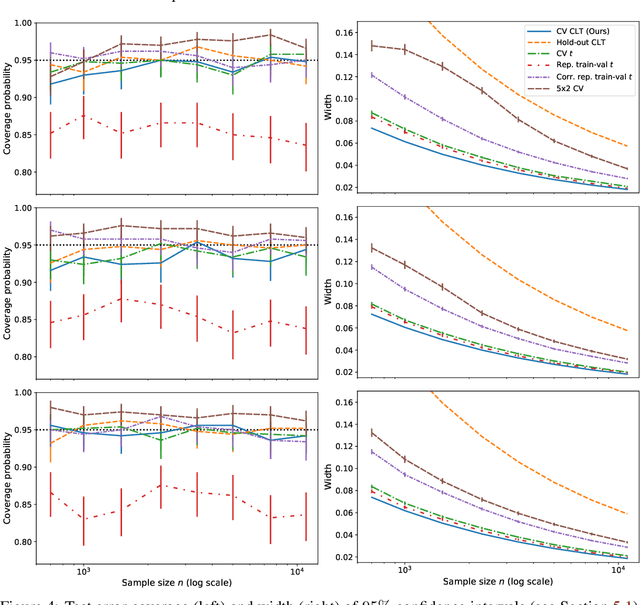
This work develops central limit theorems for cross-validation and consistent estimators of its asymptotic variance under weak stability conditions on the learning algorithm. Together, these results provide practical, asymptotically-exact confidence intervals for $k$-fold test error and valid, powerful hypothesis tests of whether one learning algorithm has smaller $k$-fold test error than another. These results are also the first of their kind for the popular choice of leave-one-out cross-validation. In our real-data experiments with diverse learning algorithms, the resulting intervals and tests outperform the most popular alternative methods from the literature.