Cross-validation Confidence Intervals for Test Error

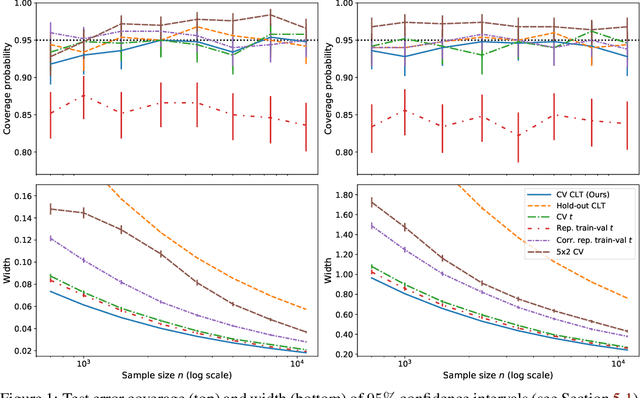
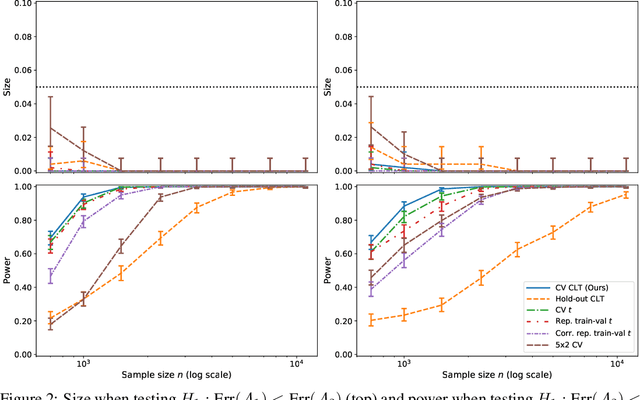
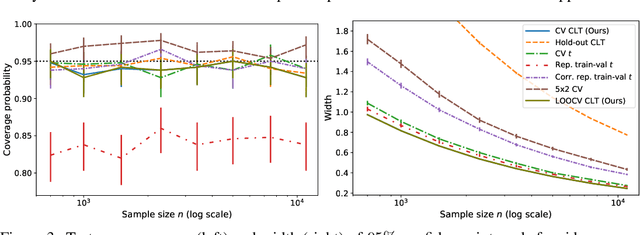
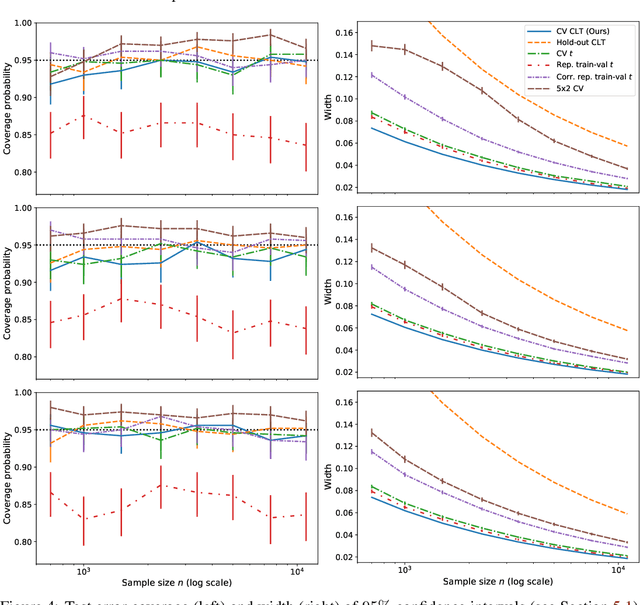
This work develops central limit theorems for cross-validation and consistent estimators of its asymptotic variance under weak stability conditions on the learning algorithm. Together, these results provide practical, asymptotically-exact confidence intervals for $k$-fold test error and valid, powerful hypothesis tests of whether one learning algorithm has smaller $k$-fold test error than another. These results are also the first of their kind for the popular choice of leave-one-out cross-validation. In our real-data experiments with diverse learning algorithms, the resulting intervals and tests outperform the most popular alternative methods from the literature.