Factor-Augmented Regularized Model for Hazard Regression
Paper and Code
Oct 03, 2022
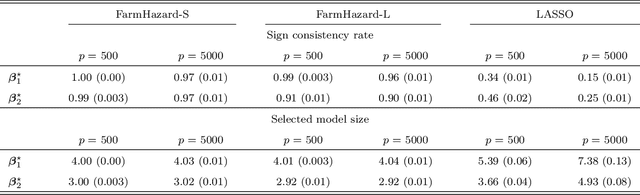
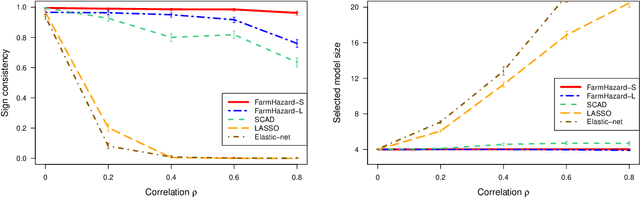
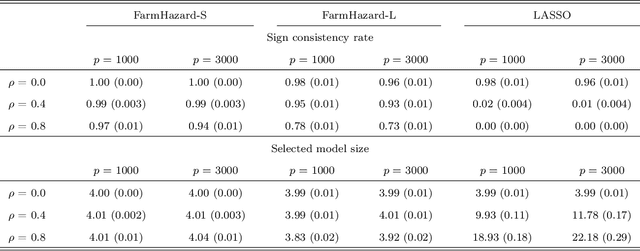
A prevalent feature of high-dimensional data is the dependence among covariates, and model selection is known to be challenging when covariates are highly correlated. To perform model selection for the high-dimensional Cox proportional hazards model in presence of correlated covariates with factor structure, we propose a new model, Factor-Augmented Regularized Model for Hazard Regression (FarmHazard), which builds upon latent factors that drive covariate dependence and extends Cox's model. This new model generates procedures that operate in two steps by learning factors and idiosyncratic components from high-dimensional covariate vectors and then using them as new predictors. Cox's model is a widely used semi-parametric model for survival analysis, where censored data and time-dependent covariates bring additional technical challenges. We prove model selection consistency and estimation consistency under mild conditions. We also develop a factor-augmented variable screening procedure to deal with strong correlations in ultra-high dimensional problems. Extensive simulations and real data experiments demonstrate that our procedures enjoy good performance and achieve better results on model selection, out-of-sample C-index and screening than alternative methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge