Efficient Long Speech Sequence Modelling for Time-Domain Depression Level Estimation

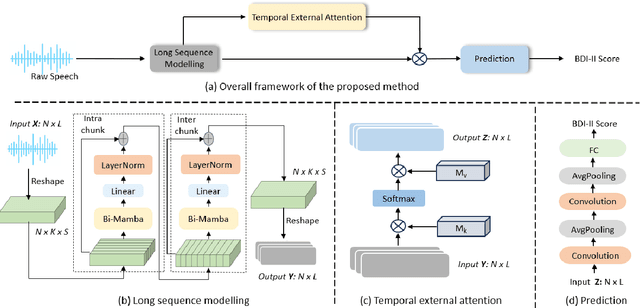
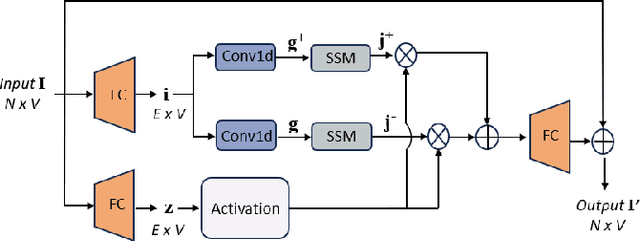
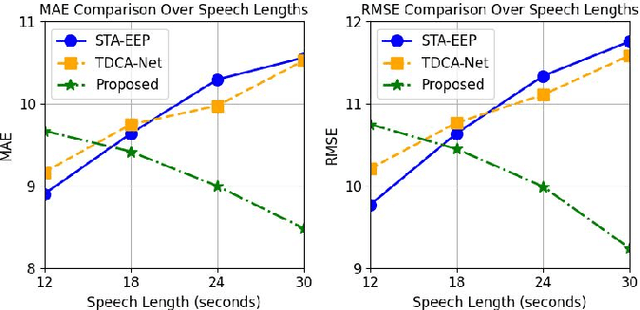
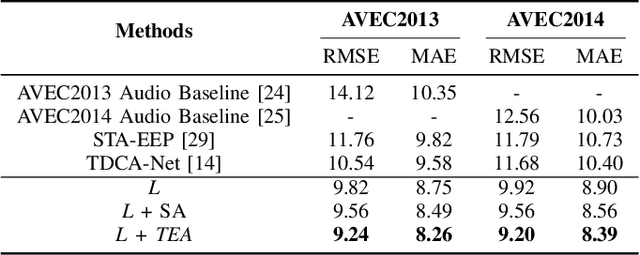
Depression significantly affects emotions, thoughts, and daily activities. Recent research indicates that speech signals contain vital cues about depression, sparking interest in audio-based deep-learning methods for estimating its severity. However, most methods rely on time-frequency representations of speech which have recently been criticized for their limitations due to the loss of information when performing time-frequency projections, e.g. Fourier transform, and Mel-scale transformation. Furthermore, segmenting real-world speech into brief intervals risks losing critical interconnections between recordings. Additionally, such an approach may not adequately reflect real-world scenarios, as individuals with depression often pause and slow down in their conversations and interactions. Building on these observations, we present an efficient method for depression level estimation using long speech signals in the time domain. The proposed method leverages a state space model coupled with the dual-path structure-based long sequence modelling module and temporal external attention module to reconstruct and enhance the detection of depression-related cues hidden in the raw audio waveforms. Experimental results on the AVEC2013 and AVEC2014 datasets show promising results in capturing consequential long-sequence depression cues and demonstrate outstanding performance over the state-of-the-art.

Client Selection for Federated Policy Optimization with Environment Heterogeneity

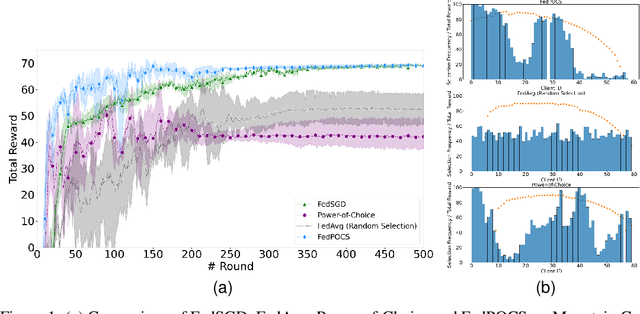
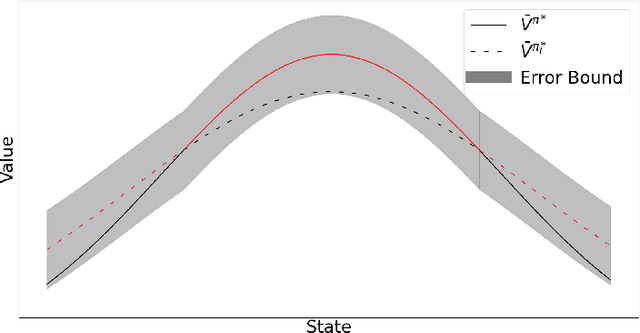
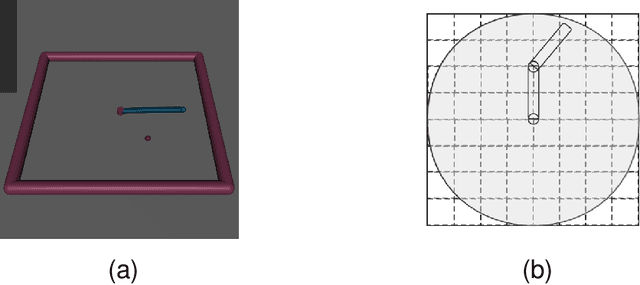
The development of Policy Iteration (PI) has inspired many recent algorithms for Reinforcement Learning (RL), including several policy gradient methods, that gained both theoretical soundness and empirical success on a variety of tasks. The theory of PI is rich in the context of centralized learning, but its study is still in the infant stage under the federated setting. This paper explores the federated version of Approximate PI (API) and derives its error bound, taking into account the approximation error introduced by environment heterogeneity. We theoretically prove that a proper client selection scheme can reduce this error bound. Based on the theoretical result, we propose a client selection algorithm to alleviate the additional approximation error caused by environment heterogeneity. Experiment results show that the proposed algorithm outperforms other biased and unbiased client selection methods on the federated mountain car problem by effectively selecting clients with a lower level of heterogeneity from the population distribution.

FedKL: Tackling Data Heterogeneity in Federated Reinforcement Learning by Penalizing KL Divergence

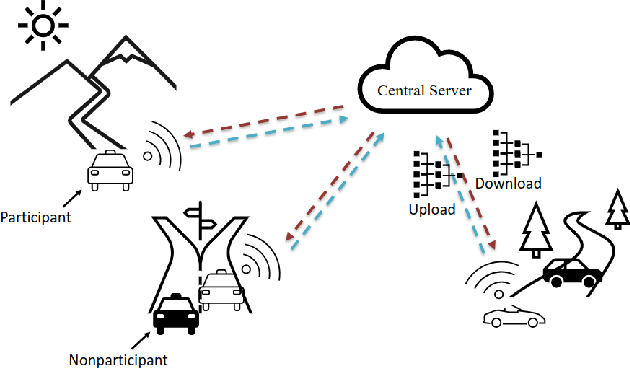
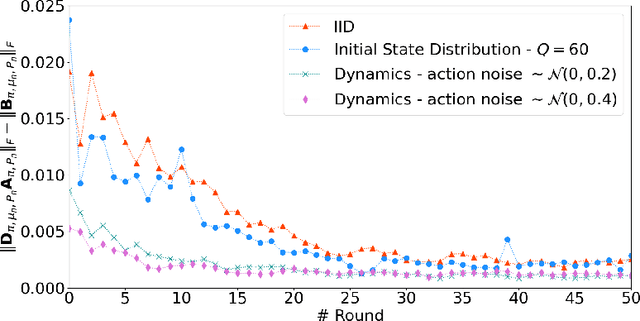
As a distributed learning paradigm, Federated Learning (FL) faces the communication bottleneck issue due to many rounds of model synchronization and aggregation. Heterogeneous data further deteriorates the situation by causing slow convergence. Although the impact of data heterogeneity on supervised FL has been widely studied, the related investigation for Federated Reinforcement Learning (FRL) is still in its infancy. In this paper, we first define the type and level of data heterogeneity for policy gradient based FRL systems. By inspecting the connection between the global and local objective functions, we prove that local training can benefit the global objective, if the local update is properly penalized by the total variation (TV) distance between the local and global policies. A necessary condition for the global policy to be learn-able from the local policy is also derived, which is directly related to the heterogeneity level. Based on the theoretical result, a Kullback-Leibler (KL) divergence based penalty is proposed, which, different from the conventional method that penalizes the model divergence in the parameter space, directly constrains the model outputs in the distribution space. By jointly penalizing the divergence of the local policy from the global policy with a global penalty and constraining each iteration of the local training with a local penalty, the proposed method achieves a better trade-off between training speed (step size) and convergence. Experiment results on two popular RL experiment platforms demonstrate the advantage of the proposed algorithm over existing methods in accelerating and stabilizing the training process with heterogeneous data.