Dual-Channel Tensor Neural Networks: Finite-Sample Theory and Conformal Structure Selection

Tensor-valued data arise naturally in neuroimaging, genomics, climate science, and spatiotemporal networks, where multilinear dependencies across modes carry information that is destroyed under vectorization. Existing approaches either impose a single low-rank structure, which can miss localized signal, or treat the tensor as a long vector, which discards its multiway geometry. We propose a *Dual-Channel Tensor Neural Network* (DC-TNN) that decomposes each tensor input into a low-rank core and a sparse refinement, and processes the two components through coupled neural channels. The framework is structure-agnostic and accommodates CP, Tucker, and tensor-train cores within a single architecture. For estimation, we establish non-asymptotic risk bounds for the DC-TNN estimator that decompose into network approximation, core estimation, and refinement-selection terms, and show that the effective dimension is determined jointly by the core rank and refinement sparsity rather than by the ambient tensor size. For inference, we develop a *structure-aware conformal ROC* procedure that calibrates within the core-refinement latent space and produces ROC and AUC confidence bands with finite-sample, distribution-free coverage. Building on this, we propose a *conformal structure selector* that, to our knowledge, is the *first distribution-free procedure* for choosing among candidate tensor decompositions with finite-sample validity. Simulations and an analysis of a protein dataset demonstrate competitive predictive accuracy, reliable uncertainty quantification, and consistent recovery of the tensor structure.

Conditional Prediction ROC Bands for Graph Classification

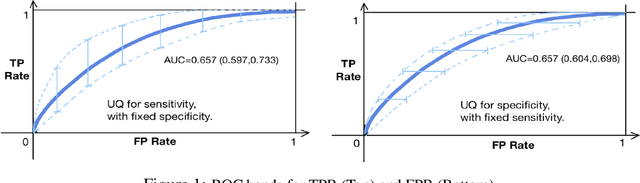
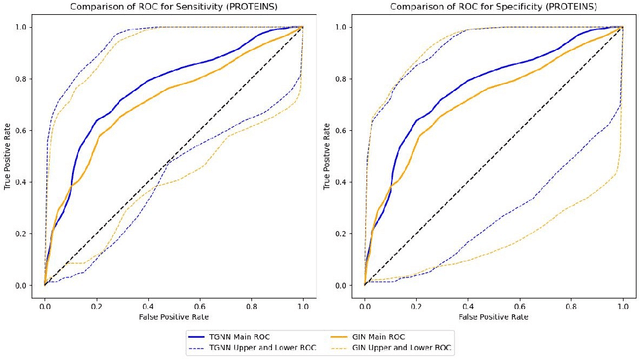
Graph classification in medical imaging and drug discovery requires accuracy and robust uncertainty quantification. To address this need, we introduce Conditional Prediction ROC (CP-ROC) bands, offering uncertainty quantification for ROC curves and robustness to distributional shifts in test data. Although developed for Tensorized Graph Neural Networks (TGNNs), CP-ROC is adaptable to general Graph Neural Networks (GNNs) and other machine learning models. We establish statistically guaranteed coverage for CP-ROC under a local exchangeability condition. This addresses uncertainty challenges for ROC curves under non-iid setting, ensuring reliability when test graph distributions differ from training data. Empirically, to establish local exchangeability for TGNNs, we introduce a data-driven approach to construct local calibration sets for graphs. Comprehensive evaluations show that CP-ROC significantly improves prediction reliability across diverse tasks. This method enhances uncertainty quantification efficiency and reliability for ROC curves, proving valuable for real-world applications with non-iid objects.

Conditional Uncertainty Quantification for Tensorized Topological Neural Networks

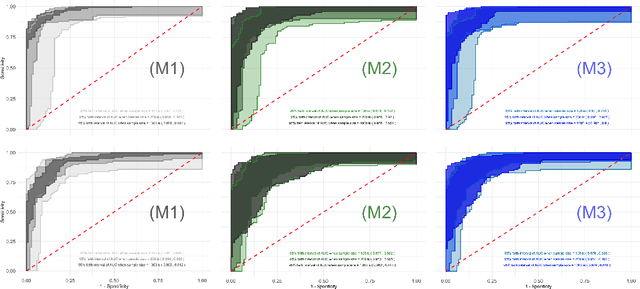
Graph Neural Networks (GNNs) have become the de facto standard for analyzing graph-structured data, leveraging message-passing techniques to capture both structural and node feature information. However, recent studies have raised concerns about the statistical reliability of uncertainty estimates produced by GNNs. This paper addresses this crucial challenge by introducing a novel technique for quantifying uncertainty in non-exchangeable graph-structured data, while simultaneously reducing the size of label prediction sets in graph classification tasks. We propose Conformalized Tensor-based Topological Neural Networks (CF-T2NN), a new approach for rigorous prediction inference over graphs. CF-T2NN employs tensor decomposition and topological knowledge learning to navigate and interpret the inherent uncertainty in decision-making processes. This method enables a more nuanced understanding and handling of prediction uncertainties, enhancing the reliability and interpretability of neural network outcomes. Our empirical validation, conducted across 10 real-world datasets, demonstrates the superiority of CF-T2NN over a wide array of state-of-the-art methods on various graph benchmarks. This work not only enhances the GNN framework with robust uncertainty quantification capabilities but also sets a new standard for reliability and precision in graph-structured data analysis.