Low-Complexity Estimation Algorithm and Decoupling Scheme for FRaC System

With the leaping advances in autonomous vehicles and transportation infrastructure, dual function radar-communication (DFRC) systems have become attractive due to the size, cost and resource efficiency. A frequency modulated continuous waveform (FMCW)-based radar-communication system (FRaC) utilizing both sparse multiple-input and multiple-output (MIMO) arrays and index modulation (IM) has been proposed to form a DFRC system specifically designed for vehicular applications. In this paper, the three-dimensional (3D) parameter estimation problem in the FRaC is considered. Since the 3D-parameters including range, direction of arrival (DOA) and velocity are coupled in the estimating matrix of the FRaC system, the existing estimation algorithms cannot estimate the 3D-parameters accurately. Hence, a novel decomposed decoupled atomic norm minimization (DANM) method is proposed by splitting the 3D-parameter estimating matrix into multiple 2D matrices with sparsity constraints. Then, the 3D-parameters are estimated and efficiently and separately with the optimized decoupled estimating matrix. Moreover, the Cram\'{e}r-Rao lower bound (CRLB) of the 3D-parameter estimation are derived, and the computational complexity of the proposed algorithm is analyzed. Simulation results show that the proposed decomposed DANM method exploits the advantage of the virtual aperture in the existence of coupling caused by IM and sparse MIMO array and outperforms the co-estimation algorithm with lower computation complexity.

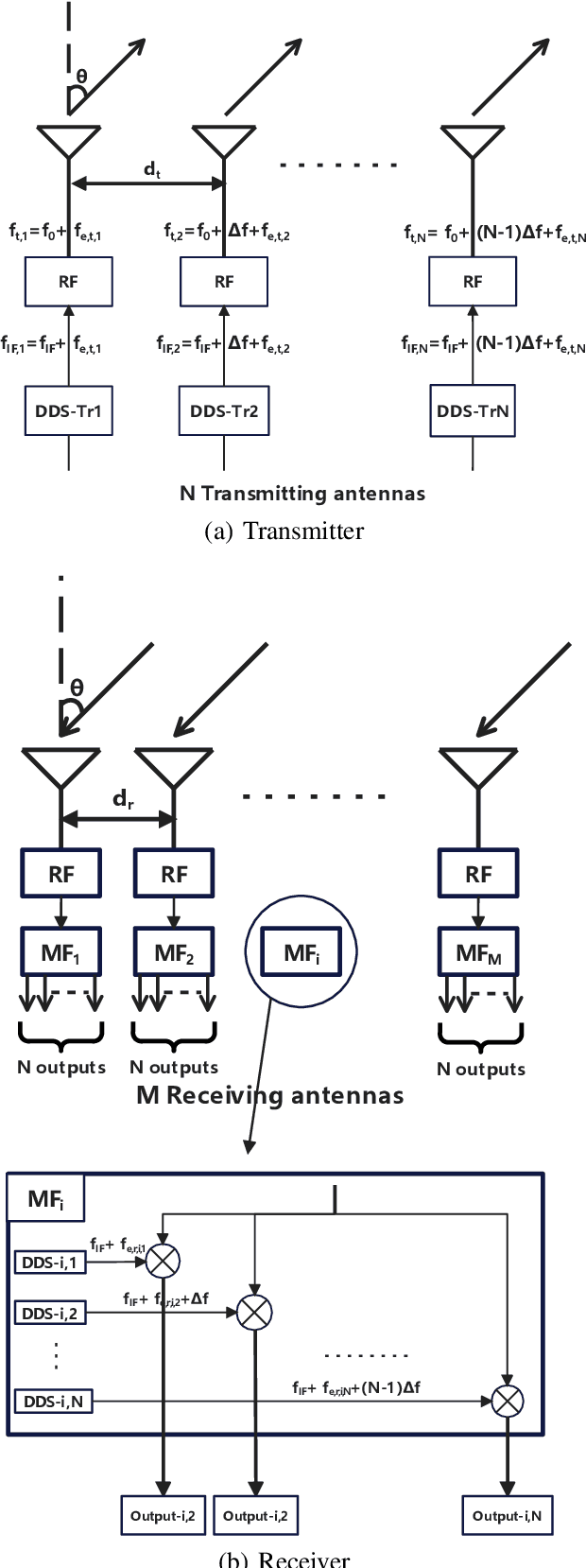
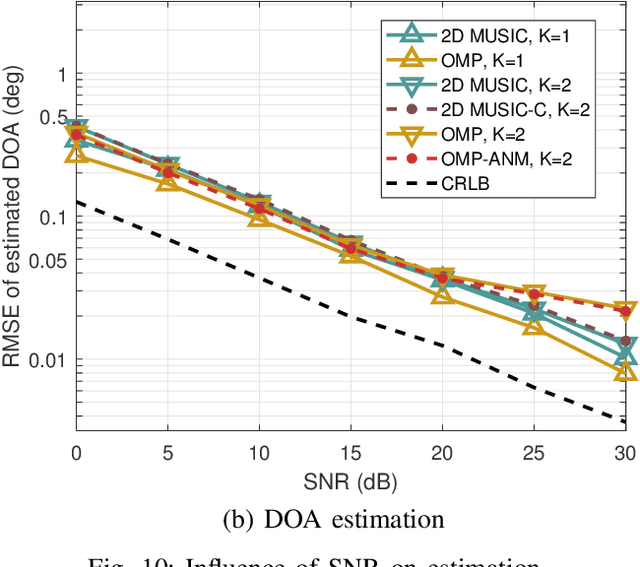
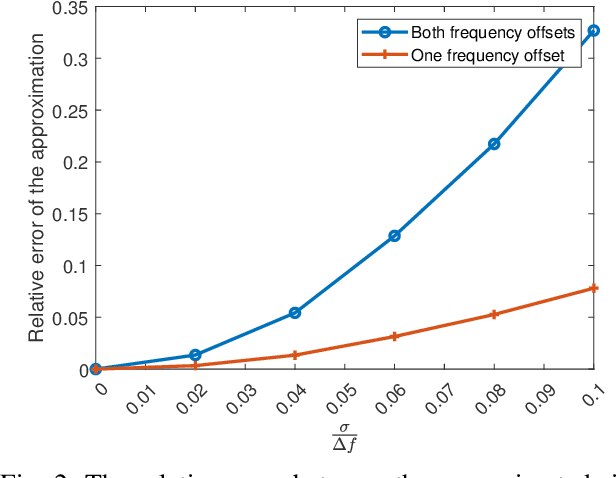
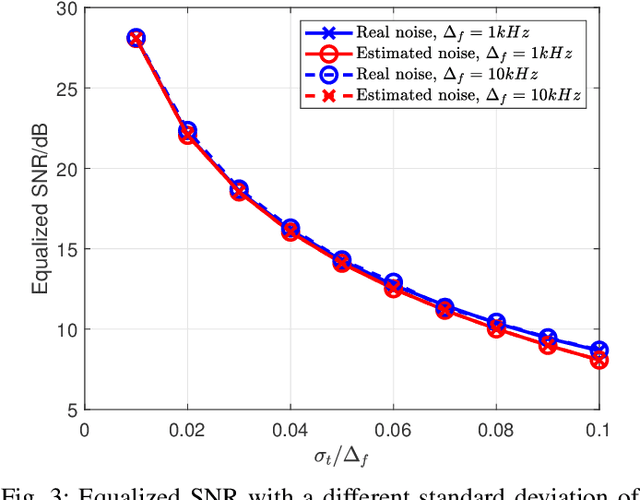
Range-Angle Estimation for FDA-MIMO System With Frequency Offset

Frequency diverse array multiple-input multiple-output (FDA-MIMO) radar differs from the traditional phased array (PA) radar, and can form range-angle-dependent beampattern and differentiate between closely spaced targets sharing the same angle but occupying distinct range cells. In the FDA-MIMO radar, target range estimation is achieved by employing a subtle frequency variation between adjacent array antennas, so the estimation performance is degraded severely in a practical scenario with frequency offset. In this paper, the range-angle estimation problem for FDA-MIMO radar is considered with frequency offsets in both transmitting and receiving arrays. First, we build a system model for the FDA-MIMO radar with transmitting and receiving frequency offsets. Then, the frequency offset is transferred into an equalized additional noise. The noise characteristics are analyzed in detail theoretically, together with the influence on the range-angle estimation. Moreover, since the effect of the transmitting frequency offset is similar to additional colored noise, denoising algorithms are introduced to mitigate the performance deterioration caused by the frequency offset. Finally, Cram\'{e}r-Rao lower bounds (CRLB) for the range-angle estimation are derived in the scenario with the frequency offsets. Simulation results show the analysis of frequency offset and the corresponding estimation performance using different algorithms.

NoncovANM: Gridless DOA Estimation for LPDF System

Direction of arrival (DOA) estimation is an important research in the area of array signal processing, and has been studied for decades. High resolution DOA estimation requires large array aperture, which leads to the increase of hardware cost. Besides, high accuracy DOA estimation methods usually have high computational complexity. In this paper, the problem of decreasing the hardware cost and algorithm complexity is addressed. First, considering the ability of flexible controlling the electromagnetic waves and low-cost, an intelligent reconfigurable surface (IRS)-aided low-cost passive direction finding (LPDF) system is developed, where only one fully functional receiving channel is adopted. Then, the sparsity of targets direction in the spatial domain is exploited by formulating an atomic norm minimization (ANM) problem to estimate the DOA. Traditionally, solving ANM problem is complex and cannot be realized efficiently. Hence, a novel nonconvex-based ANM (NC-ANM) method is proposed by gradient threshold iteration, where a perturbation is introduced to avoid falling into saddle points. The theoretical analysis for the convergence of the NC-ANM method is also given. Moreover, the corresponding Cram\'er-Rao lower bound (CRLB) in the LPDF system is derived, and taken as the referred bound of the DOA estimation. Simulation results show that the proposed method outperforms the compared methods in the DOA estimation with lower computational complexity in the LPDF system.

URGLQ: An Efficient Covariance Matrix Reconstruction Method for Robust Adaptive Beamforming

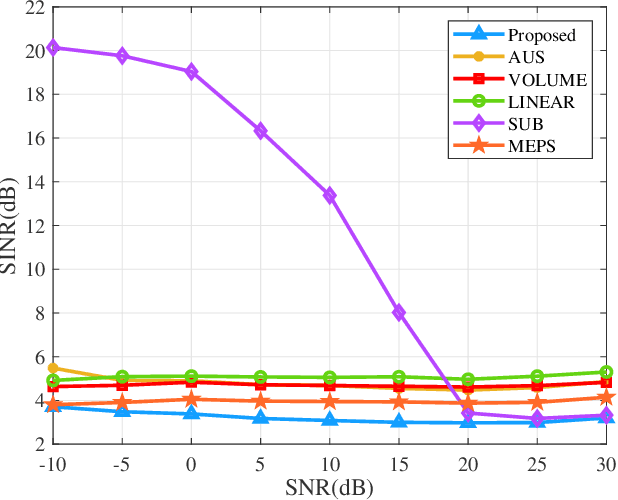
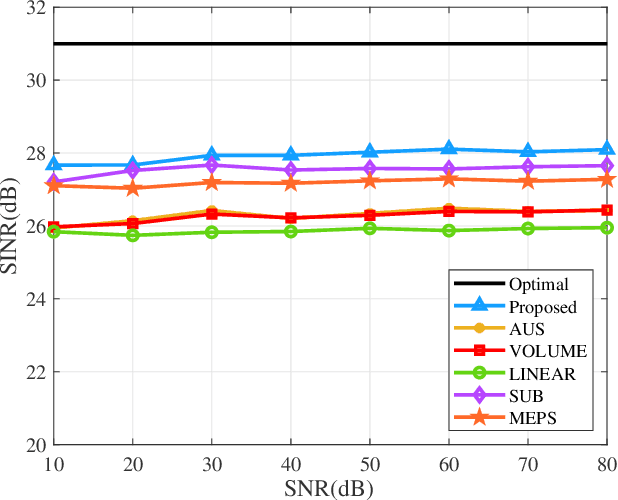
The computational complexity of the conventional adaptive beamformer is relatively large, and the performance degrades significantly due to both the model mismatch errors and the unwanted signals in received data. In this paper, an efficient unwanted signal removal and Gauss-Legendre quadrature (URGLQ)-based covariance matrix reconstruction method is proposed. Different from the prior covariance matrix reconstruction methods, a projection matrix is constructed to remove the unwanted signal from the received data, which improves the reconstruction accuracy of the covariance matrix. Considering that the computational complexity of most matrix reconstruction algorithms are relatively large due to the integral operation, we proposed a Gauss-Legendre quadrature-based method to approximate the integral operation while maintaining the accuracy. Moreover, to improve the robustness of the beamformer, the mismatch in the desired steering vector is corrected by maximizing the output power of the beamformer under a constraint that the corrected steering vector cannot converge to any interference steering vector. Simulation results and prototype experiment demonstrate that the performance of the proposed beamformer outperforms the compared methods and is much closer to the optimal beamformer in different scenarios.