Zhengli Xing
Low-Rank Phase Retrieval via Variational Bayesian Learning
Nov 05, 2018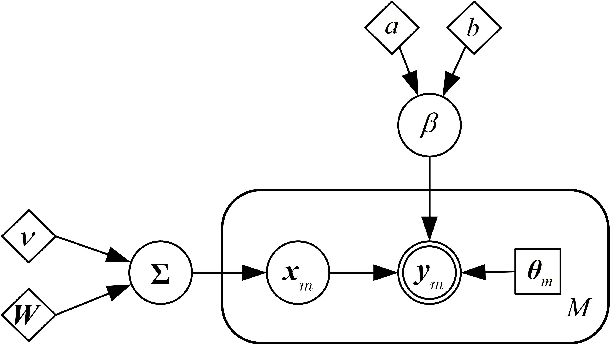
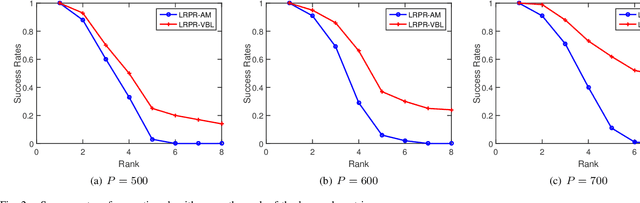
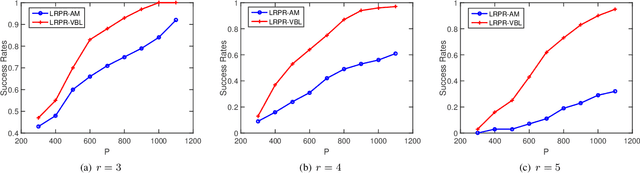
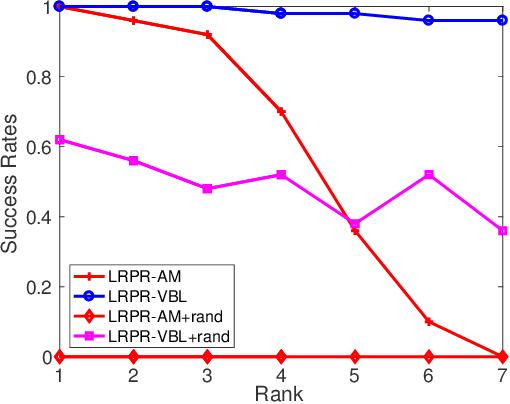
Abstract:In this paper, we consider the problem of low-rank phase retrieval whose objective is to estimate a complex low-rank matrix from magnitude-only measurements. We propose a hierarchical prior model for low-rank phase retrieval, in which a Gaussian-Wishart hierarchical prior is placed on the underlying low-rank matrix to promote the low-rankness of the matrix. Based on the proposed hierarchical model, a variational expectation-maximization (EM) algorithm is developed. The proposed method is less sensitive to the choice of the initialization point and works well with random initialization. Simulation results are provided to illustrate the effectiveness of the proposed algorithm.
Simultaneous Block-Sparse Signal Recovery Using Pattern-Coupled Sparse Bayesian Learning
Nov 06, 2017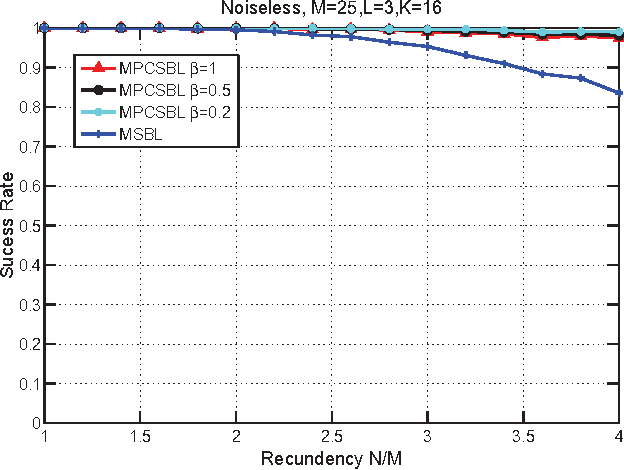
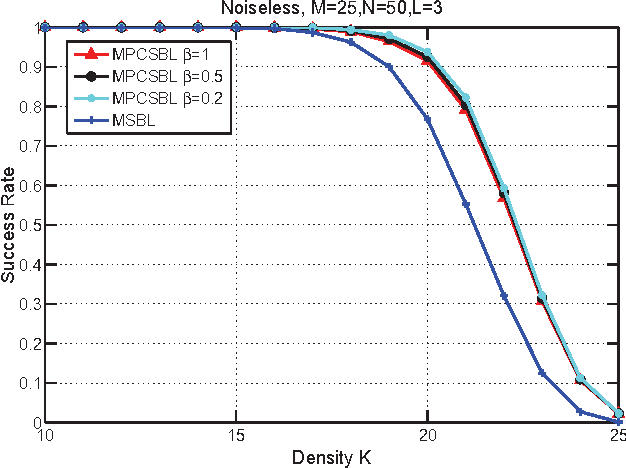
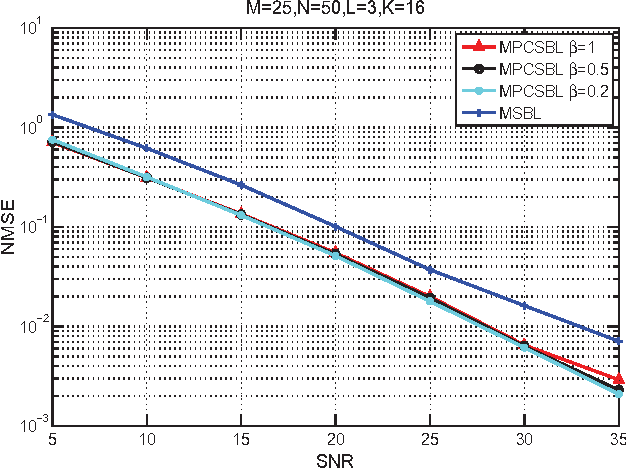
Abstract:In this paper, we consider the block-sparse signals recovery problem in the context of multiple measurement vectors (MMV) with common row sparsity patterns. We develop a new method for recovery of common row sparsity MMV signals, where a pattern-coupled hierarchical Gaussian prior model is introduced to characterize both the block-sparsity of the coefficients and the statistical dependency between neighboring coefficients of the common row sparsity MMV signals. Unlike many other methods, the proposed method is able to automatically capture the block sparse structure of the unknown signal. Our method is developed using an expectation-maximization (EM) framework. Simulation results show that our proposed method offers competitive performance in recovering block-sparse common row sparsity pattern MMV signals.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge