Kaihui Liu
Low-Rank Phase Retrieval via Variational Bayesian Learning
Nov 05, 2018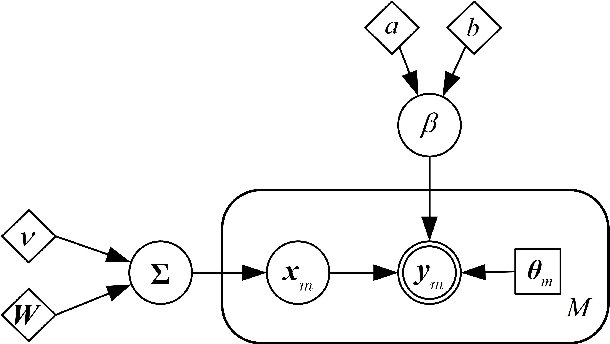
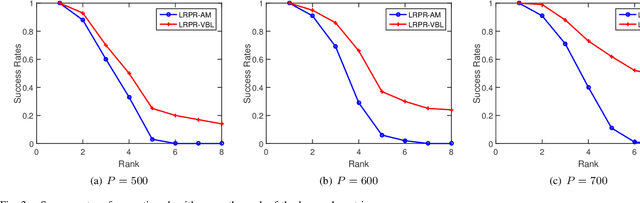
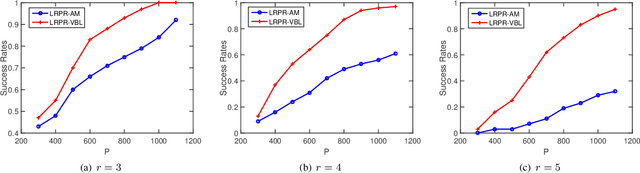
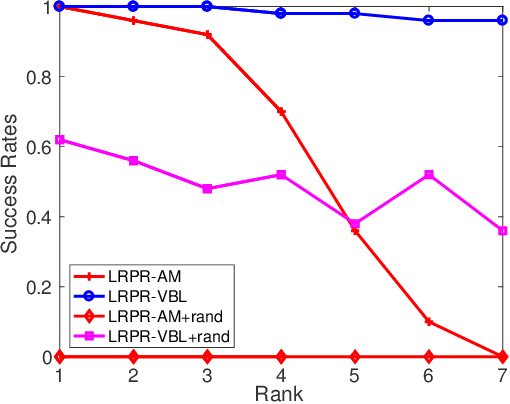
Abstract:In this paper, we consider the problem of low-rank phase retrieval whose objective is to estimate a complex low-rank matrix from magnitude-only measurements. We propose a hierarchical prior model for low-rank phase retrieval, in which a Gaussian-Wishart hierarchical prior is placed on the underlying low-rank matrix to promote the low-rankness of the matrix. Based on the proposed hierarchical model, a variational expectation-maximization (EM) algorithm is developed. The proposed method is less sensitive to the choice of the initialization point and works well with random initialization. Simulation results are provided to illustrate the effectiveness of the proposed algorithm.
Bayesian Compressive Sensing Using Normal Product Priors
Aug 24, 2017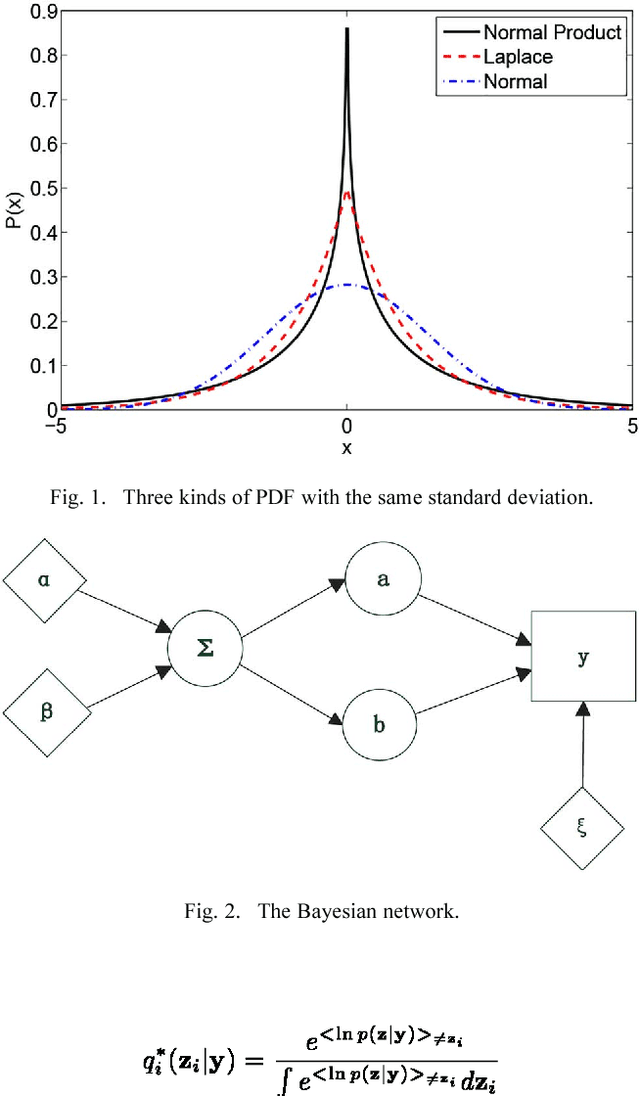
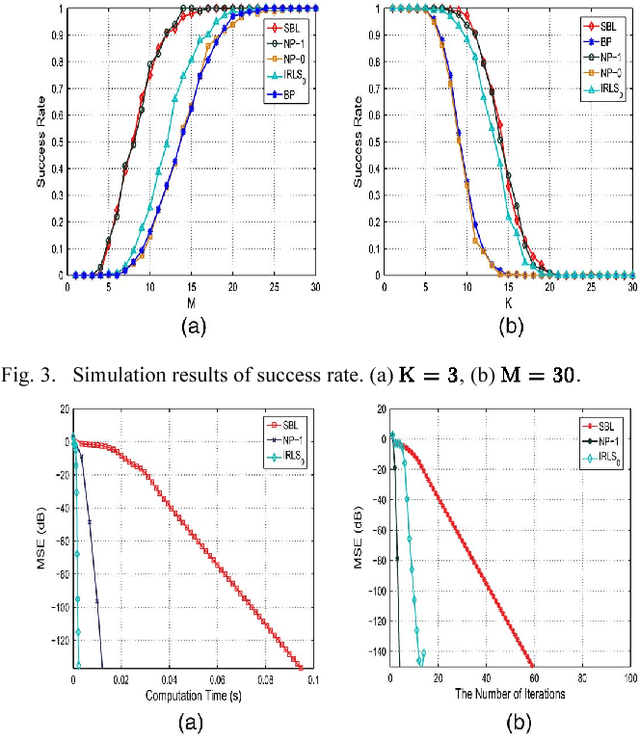
Abstract:In this paper, we introduce a new sparsity-promoting prior, namely, the "normal product" prior, and develop an efficient algorithm for sparse signal recovery under the Bayesian framework. The normal product distribution is the distribution of a product of two normally distributed variables with zero means and possibly different variances. Like other sparsity-encouraging distributions such as the Student's $t$-distribution, the normal product distribution has a sharp peak at origin, which makes it a suitable prior to encourage sparse solutions. A two-stage normal product-based hierarchical model is proposed. We resort to the variational Bayesian (VB) method to perform the inference. Simulations are conducted to illustrate the effectiveness of our proposed algorithm as compared with other state-of-the-art compressed sensing algorithms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge