Kalman Filter Auto-tuning through Enforcing Chi-Squared Normalized Error Distributions with Bayesian Optimization

The nonlinear and stochastic relationship between noise covariance parameter values and state estimator performance makes optimal filter tuning a very challenging problem. Popular optimization-based tuning approaches can easily get trapped in local minima, leading to poor noise parameter identification and suboptimal state estimation. Recently, black box techniques based on Bayesian optimization with Gaussian processes (GPBO) have been shown to overcome many of these issues, using normalized estimation error squared (NEES) and normalized innovation error (NIS) statistics to derive cost functions for Kalman filter auto-tuning. While reliable noise parameter estimates are obtained in many cases, GPBO solutions obtained with these conventional cost functions do not always converge to optimal filter noise parameters and lack robustness to parameter ambiguities in time-discretized system models. This paper addresses these issues by making two main contributions. First, we show that NIS and NEES errors are only chi-squared distributed for tuned estimators. As a result, chi-square tests are not sufficient to ensure that an estimator has been correctly tuned. We use this to extend the familiar consistency tests for NIS and NEES to penalize if the distribution is not chi-squared distributed. Second, this cost measure is applied within a Student-t processes Bayesian Optimization (TPBO) to achieve robust estimator performance for time discretized state space models. The robustness, accuracy, and reliability of our approach are illustrated on classical state estimation problems.

Kalman Filter Tuning with Bayesian Optimization

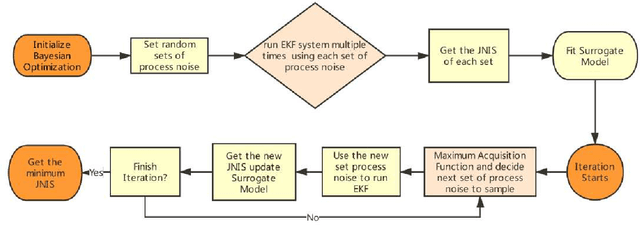
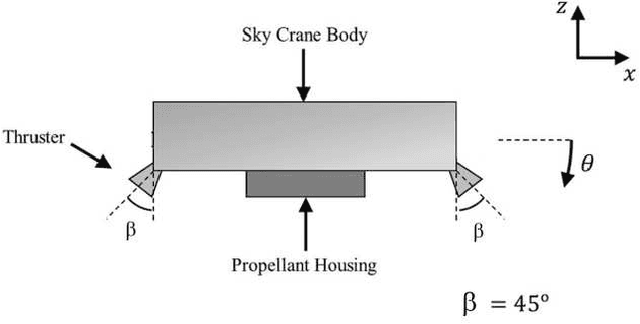
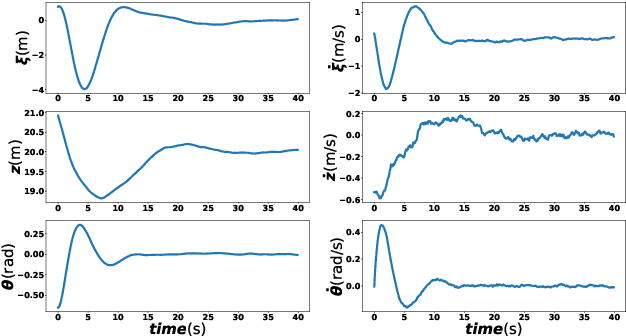
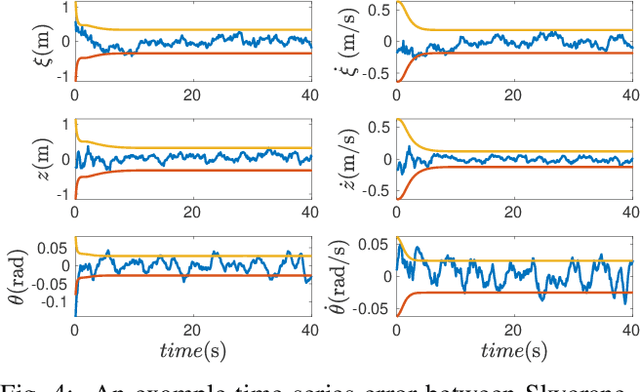
Many state estimation algorithms must be tuned given the state space process and observation models, the process and observation noise parameters must be chosen. Conventional tuning approaches rely on heuristic hand-tuning or gradient-based optimization techniques to minimize a performance cost function. However, the relationship between tuned noise values and estimator performance is highly nonlinear and stochastic. Therefore, the tuning solutions can easily get trapped in local minima, which can lead to poor choices of noise parameters and suboptimal estimator performance. This paper describes how Bayesian Optimization (BO) can overcome these issues. BO poses optimization as a Bayesian search problem for a stochastic ``black box'' cost function, where the goal is to search the solution space to maximize the probability of improving the current best solution. As such, BO offers a principled approach to optimization-based estimator tuning in the presence of local minima and performance stochasticity. While extended Kalman filters (EKFs) are the main focus of this work, BO can be similarly used to tune other related state space filters. The method presented here uses performance metrics derived from normalized innovation squared (NIS) filter residuals obtained via sensor data, which renders knowledge of ground-truth states unnecessary. The robustness, accuracy, and reliability of BO-based tuning is illustrated on practical nonlinear state estimation problems,losed-loop aero-robotic control.

Weak in the NEES?: Auto-tuning Kalman Filters with Bayesian Optimization

Kalman filters are routinely used for many data fusion applications including navigation, tracking, and simultaneous localization and mapping problems. However, significant time and effort is frequently required to tune various Kalman filter model parameters, e.g. process noise covariance, pre-whitening filter models for non-white noise, etc. Conventional optimization techniques for tuning can get stuck in poor local minima and can be expensive to implement with real sensor data. To address these issues, a new "black box" Bayesian optimization strategy is developed for automatically tuning Kalman filters. In this approach, performance is characterized by one of two stochastic objective functions: normalized estimation error squared (NEES) when ground truth state models are available, or the normalized innovation error squared (NIS) when only sensor data is available. By intelligently sampling the parameter space to both learn and exploit a nonparametric Gaussian process surrogate function for the NEES/NIS costs, Bayesian optimization can efficiently identify multiple local minima and provide uncertainty quantification on its results.