A Unified Issue Resolution Benchmark for Requirement Clarification, Planning, and Code Generation for Coding Agents

Large language model-powered coding agents are increasingly used to modify existing code repositories, for example, by adding features or fixing bugs. Yet existing repository-level benchmarks typically evaluate only whether the final patch passes tests. Satisfying a user request requires a long chain of interdependent reasoning and decisions: an agent must recover explicit and implicit requirements, formulate a repository-grounded implementation plan, and translate it into correct code. A pass/fail outcome cannot characterize how an unsuccessful trajectory diverges from the requirements and implementation process needed for a correct patch. To address this gap, we introduce SWE-RPG, a repository-level benchmark that combines executable patch evaluation with validated ground-truth references (GTs) for (1) Requirement Clarification and (2) Implementation Planning. These intermediate GTs support retrospective, GT-aligned diagnosis of complete coding-agent trajectories across clarification, planning, code generation, and artifact submission. SWE-RPG comprises 163 tasks from 31 Python and Java repositories, including 113 bug fixes and 50 feature additions. We evaluate 3 coding agents, including Claude Code, Codex, and OpenCode, with 6 large language model backends, including Claude-Sonnet-5 and GPT-5.6-Terra. Results show that the evaluated popular coding agents still struggle to implement user requests in existing repositories, achieving an average resolved rate of only 31.5% on SWE-RPG. Intermediate-GT diagnosis further identifies implicit requirement recovery as the main bottleneck, accounting for 24.5%--46.0% of agent runs. This result suggests implicit-requirement recovery as a key candidate direction for improving coding agents. The benchmark data and evaluation code are available at https://github.com/Xin-Zhou-smu/SWE-RPG-Bench.

ComBench: A Repo-level Real-world Benchmark for Compilation Error Repair

Compilation errors pose pervasive and critical challenges in software development, significantly hindering productivity. Therefore, Automated Compilation Error Repair (ACER) techniques are proposed to mitigate these issues. Despite recent advancements in ACER, its real-world performance remains poorly evaluated. This can be largely attributed to the limitations of existing benchmarks, \ie decontextualized single-file data, lack of authentic source diversity, and biased local task modeling that ignores crucial repository-level complexities. To bridge this critical gap, we propose ComBench, the first repository-level, reproducible real-world benchmark for C/C++ compilation error repair. ComBench is constructed through a novel, automated framework that systematically mines real-world failures from the GitHub CI histories of large-scale open-source projects. Our framework contributes techniques for the high-precision identification of ground-truth repair patches from complex version histories and a high-fidelity mechanism for reproducing the original, ephemeral build environments. To ensure data quality, all samples in ComBench are execution-verified -- guaranteeing reproducible failures and build success with ground-truth patches. Using ComBench, we conduct a comprehensive evaluation of 12 modern LLMs under both direct and agent-based repair settings. Our experiments reveal a significant gap between a model's ability to achieve syntactic correctness (a 73% success rate for GPT-5) and its ability to ensure semantic correctness (only 41% of its patches are valid). We also find that different models exhibit distinct specializations for different error types. ComBench provides a robust and realistic platform to guide the future development of ACER techniques capable of addressing the complexities of modern software development.

Decoupled Self-supervised Learning for Non-Homophilous Graphs

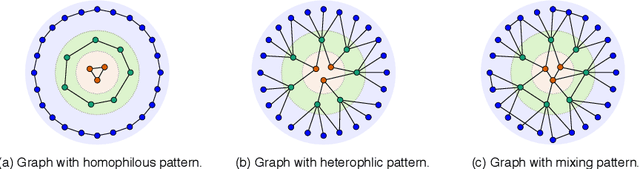
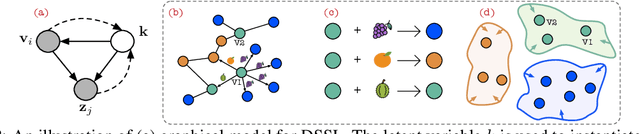
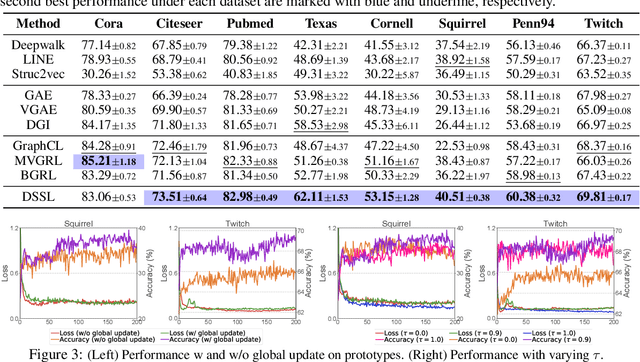
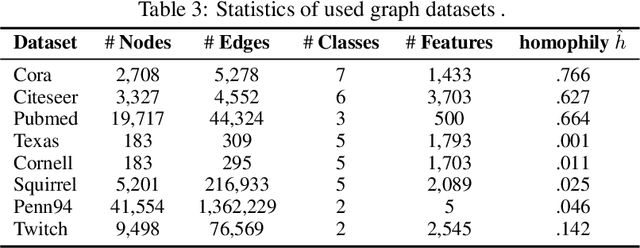
In this paper, we study the problem of conducting self-supervised learning for node representation learning on non-homophilous graphs. Existing self-supervised learning methods typically assume the graph is homophilous where linked nodes often belong to the same class or have similar features. However, such assumptions of homophily do not always hold true in real-world graphs. We address this problem by developing a decoupled self-supervised learning (DSSL) framework for graph neural networks. DSSL imitates a generative process of nodes and links from latent variable modeling of the semantic structure, which decouples different underlying semantics between different neighborhoods into the self-supervised node learning process. Our DSSL framework is agnostic to the encoders and does not need prefabricated augmentations, thus is flexible to different graphs. To effectively optimize the framework with latent variables, we derive the evidence lower-bound of the self-supervised objective and develop a scalable training algorithm with variational inference. We provide a theoretical analysis to justify that DSSL enjoys better downstream performance. Extensive experiments on various types of graph benchmarks demonstrate that our proposed framework can significantly achieve better performance compared with competitive self-supervised learning baselines.