Decoupled Self-supervised Learning for Non-Homophilous Graphs
Paper and Code
Jun 07, 2022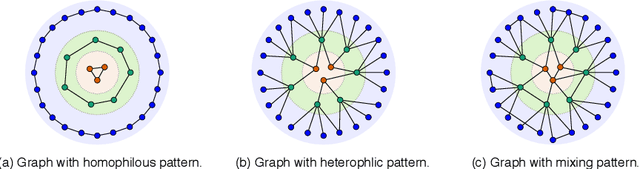
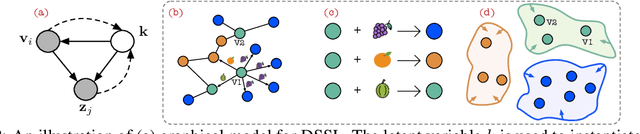
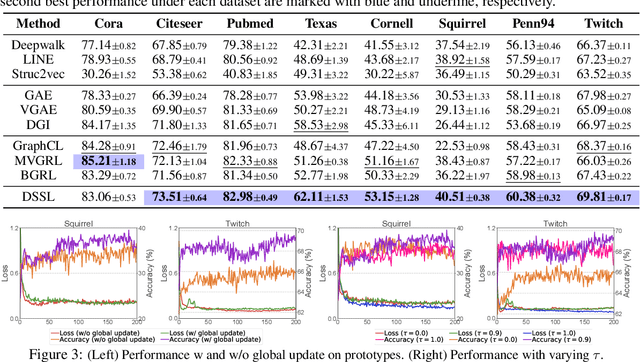
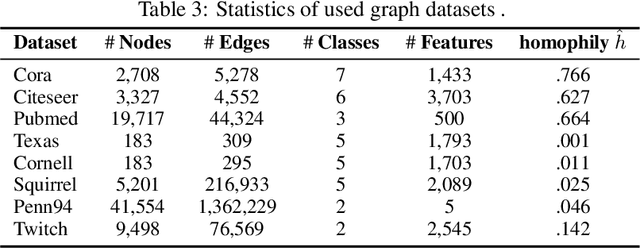
In this paper, we study the problem of conducting self-supervised learning for node representation learning on non-homophilous graphs. Existing self-supervised learning methods typically assume the graph is homophilous where linked nodes often belong to the same class or have similar features. However, such assumptions of homophily do not always hold true in real-world graphs. We address this problem by developing a decoupled self-supervised learning (DSSL) framework for graph neural networks. DSSL imitates a generative process of nodes and links from latent variable modeling of the semantic structure, which decouples different underlying semantics between different neighborhoods into the self-supervised node learning process. Our DSSL framework is agnostic to the encoders and does not need prefabricated augmentations, thus is flexible to different graphs. To effectively optimize the framework with latent variables, we derive the evidence lower-bound of the self-supervised objective and develop a scalable training algorithm with variational inference. We provide a theoretical analysis to justify that DSSL enjoys better downstream performance. Extensive experiments on various types of graph benchmarks demonstrate that our proposed framework can significantly achieve better performance compared with competitive self-supervised learning baselines.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge