Model-based clustering using non-parametric Hidden Markov Models

Thanks to their dependency structure, non-parametric Hidden Markov Models (HMMs) are able to handle model-based clustering without specifying group distributions. The aim of this work is to study the Bayes risk of clustering when using HMMs and to propose associated clustering procedures. We first give a result linking the Bayes risk of classification and the Bayes risk of clustering, which we use to identify the key quantity determining the difficulty of the clustering task. We also give a proof of this result in the i.i.d. framework, which might be of independent interest. Then we study the excess risk of the plugin classifier. All these results are shown to remain valid in the online setting where observations are clustered sequentially. Simulations illustrate our findings.

Fundamental limits for learning hidden Markov model parameters

We study the frontier between learnable and unlearnable hidden Markov models (HMMs). HMMs are flexible tools for clustering dependent data coming from unknown populations. The model parameters are known to be identifiable as soon as the clusters are distinct and the hidden chain is ergodic with a full rank transition matrix. In the limit as any one of these conditions fails, it becomes impossible to identify parameters. For a chain with two hidden states we prove nonasymptotic minimax upper and lower bounds, matching up to constants, which exhibit thresholds at which the parameters become learnable.

Risk of the Least Squares Minimum Norm Estimator under the Spike Covariance Model

We study risk of the minimum norm linear least squares estimator in when the number of parameters $d$ depends on $n$, and $\frac{d}{n} \rightarrow \infty$. We assume that data has an underlying low rank structure by restricting ourselves to spike covariance matrices, where a fixed finite number of eigenvalues grow with $n$ and are much larger than the rest of the eigenvalues, which are (asymptotically) in the same order. We show that in this setting risk of minimum norm least squares estimator vanishes in compare to risk of the null estimator. We give asymptotic and non asymptotic upper bounds for this risk, and also leverage the assumption of spike model to give an analysis of the bias that leads to tighter bounds in compare to previous works.

Exchangeable modelling of relational data: checking sparsity, train-test splitting, and sparse exchangeable Poisson matrix factorization

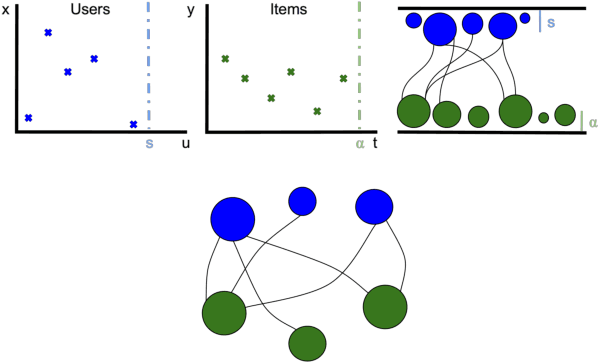
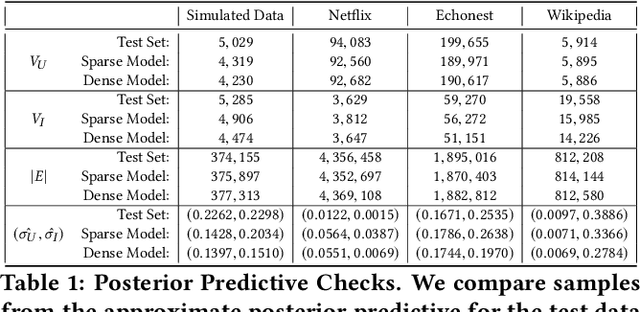
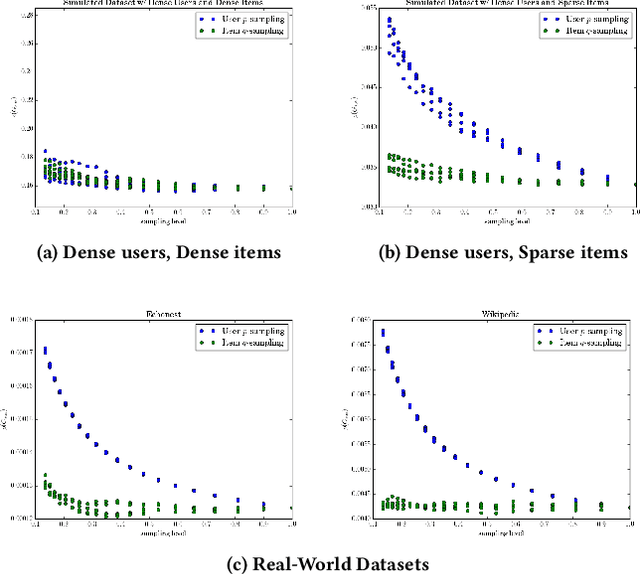
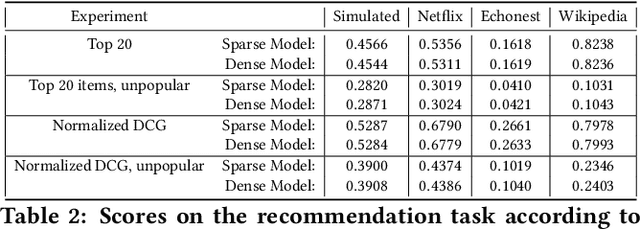
A variety of machine learning tasks---e.g., matrix factorization, topic modelling, and feature allocation---can be viewed as learning the parameters of a probability distribution over bipartite graphs. Recently, a new class of models for networks, the sparse exchangeable graphs, have been introduced to resolve some important pathologies of traditional approaches to statistical network modelling; most notably, the inability to model sparsity (in the asymptotic sense). The present paper explains some practical insights arising from this work. We first show how to check if sparsity is relevant for modelling a given (fixed size) dataset by using network subsampling to identify a simple signature of sparsity. We discuss the implications of the (sparse) exchangeable subsampling theory for test-train dataset splitting; we argue common approaches can lead to biased results, and we propose a principled alternative. Finally, we study sparse exchangeable Poisson matrix factorization as a worked example. In particular, we show how to adapt mean field variational inference to the sparse exchangeable setting, allowing us to scale inference to huge datasets.