Exchangeable modelling of relational data: checking sparsity, train-test splitting, and sparse exchangeable Poisson matrix factorization
Paper and Code
Dec 06, 2017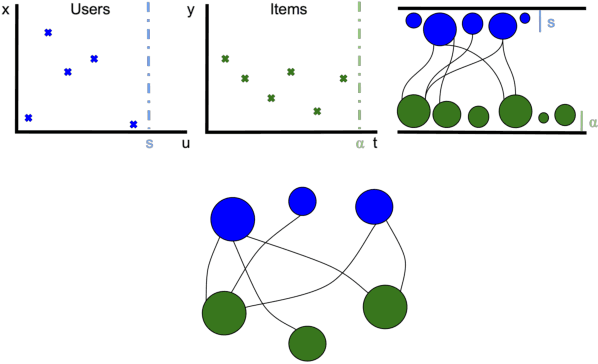
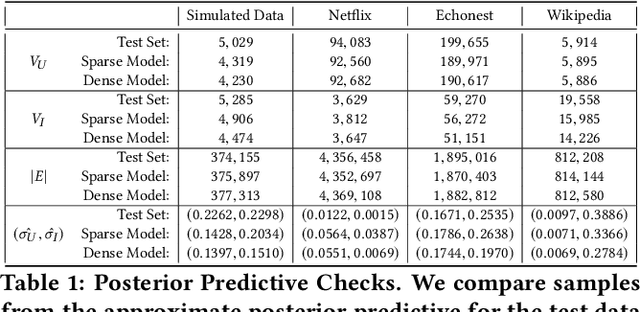
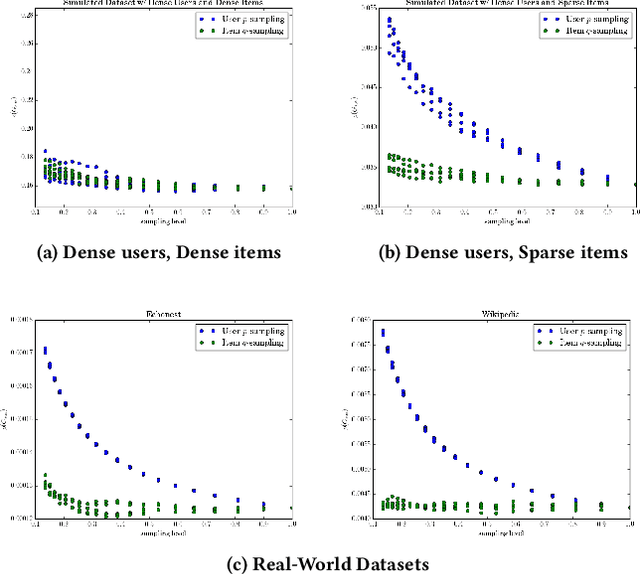
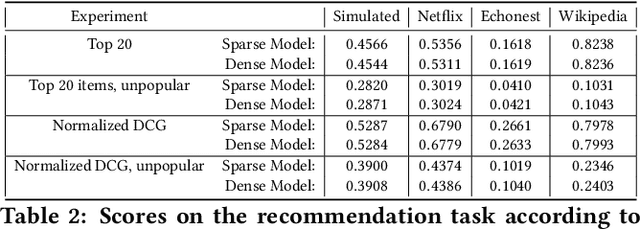
A variety of machine learning tasks---e.g., matrix factorization, topic modelling, and feature allocation---can be viewed as learning the parameters of a probability distribution over bipartite graphs. Recently, a new class of models for networks, the sparse exchangeable graphs, have been introduced to resolve some important pathologies of traditional approaches to statistical network modelling; most notably, the inability to model sparsity (in the asymptotic sense). The present paper explains some practical insights arising from this work. We first show how to check if sparsity is relevant for modelling a given (fixed size) dataset by using network subsampling to identify a simple signature of sparsity. We discuss the implications of the (sparse) exchangeable subsampling theory for test-train dataset splitting; we argue common approaches can lead to biased results, and we propose a principled alternative. Finally, we study sparse exchangeable Poisson matrix factorization as a worked example. In particular, we show how to adapt mean field variational inference to the sparse exchangeable setting, allowing us to scale inference to huge datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge