Normalized Flat Minima: Exploring Scale Invariant Definition of Flat Minima for Neural Networks using PAC-Bayesian Analysis

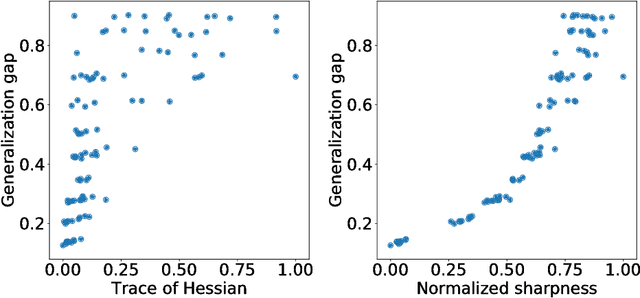
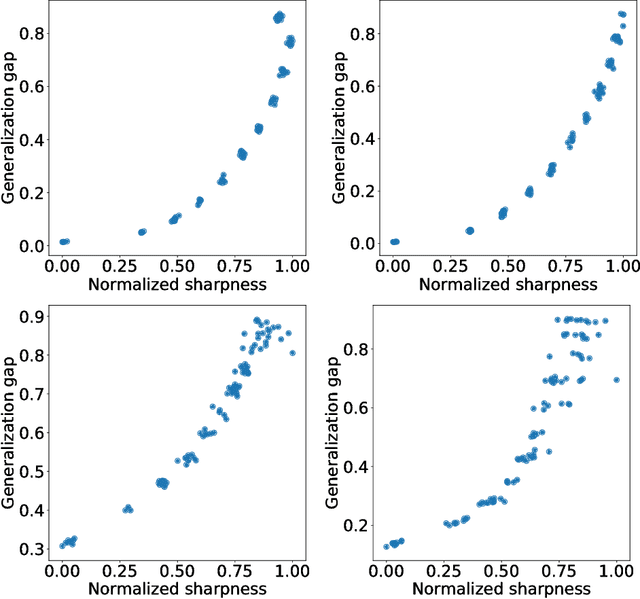
The notion of flat minima has played a key role in the generalization studies of deep learning models. However, existing definitions of the flatness are known to be sensitive to the rescaling of parameters. The issue suggests that the previous definitions of the flatness might not be a good measure of generalization, because generalization is invariant to such rescalings. In this paper, from the PAC-Bayesian perspective, we scrutinize the discussion concerning the flat minima and introduce the notion of normalized flat minima, which is free from the known scale dependence issues. Additionally, we highlight the scale dependence of existing matrix-norm based generalization error bounds similar to the existing flat minima definitions. Our modified notion of the flatness does not suffer from the insufficiency, either, suggesting it might provide better hierarchy in the hypothesis class.

Lipschitz-Margin Training: Scalable Certification of Perturbation Invariance for Deep Neural Networks

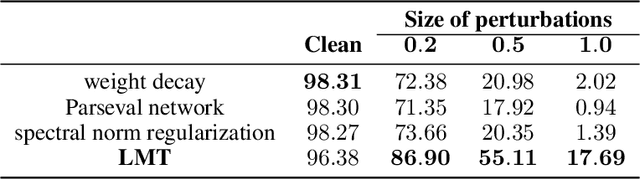
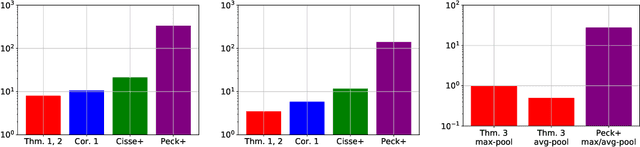
High sensitivity of neural networks against malicious perturbations on inputs causes security concerns. To take a steady step towards robust classifiers, we aim to create neural network models provably defended from perturbations. Prior certification work requires strong assumptions on network structures and massive computational costs, and thus the range of their applications was limited. From the relationship between the Lipschitz constants and prediction margins, we present a computationally efficient calculation technique to lower-bound the size of adversarial perturbations that can deceive networks, and that is widely applicable to various complicated networks. Moreover, we propose an efficient training procedure that robustifies networks and significantly improves the provably guarded areas around data points. In experimental evaluations, our method showed its ability to provide a non-trivial guarantee and enhance robustness for even large networks.

On the Structural Sensitivity of Deep Convolutional Networks to the Directions of Fourier Basis Functions

Data-agnostic quasi-imperceptible perturbations on inputs can severely degrade recognition accuracy of deep convolutional networks. This indicates some structural instability of their predictions and poses a potential security threat. However, characterization of the shared directions of such harmful perturbations remains unknown if they exist, which makes it difficult to address the security threat and performance degradation. Our primal finding is that convolutional networks are sensitive to the directions of Fourier basis functions. We derived the property by specializing a hypothesis of the cause of the sensitivity, known as the linearity of neural networks, to convolutional networks and empirically validated it. As a by-product of the analysis, we propose a fast algorithm to create shift-invariant universal adversarial perturbations available in black-box settings.

Variance-based Gradient Compression for Efficient Distributed Deep Learning

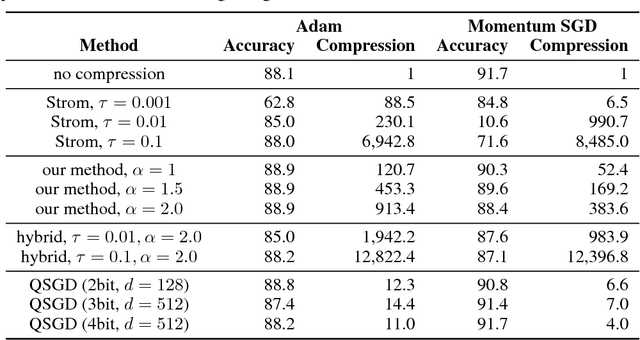
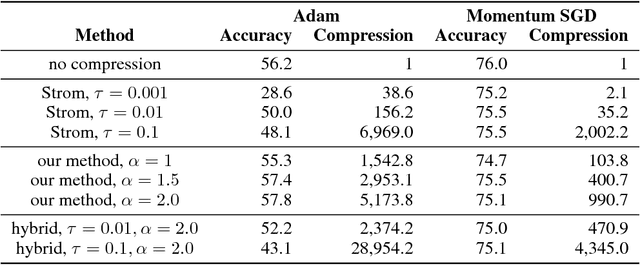
Due to the substantial computational cost, training state-of-the-art deep neural networks for large-scale datasets often requires distributed training using multiple computation workers. However, by nature, workers need to frequently communicate gradients, causing severe bottlenecks, especially on lower bandwidth connections. A few methods have been proposed to compress gradient for efficient communication, but they either suffer a low compression ratio or significantly harm the resulting model accuracy, particularly when applied to convolutional neural networks. To address these issues, we propose a method to reduce the communication overhead of distributed deep learning. Our key observation is that gradient updates can be delayed until an unambiguous (high amplitude, low variance) gradient has been calculated. We also present an efficient algorithm to compute the variance with negligible additional cost. We experimentally show that our method can achieve very high compression ratio while maintaining the result model accuracy. We also analyze the efficiency using computation and communication cost models and provide the evidence that this method enables distributed deep learning for many scenarios with commodity environments.