Normalized Flat Minima: Exploring Scale Invariant Definition of Flat Minima for Neural Networks using PAC-Bayesian Analysis
Paper and Code
Jan 28, 2019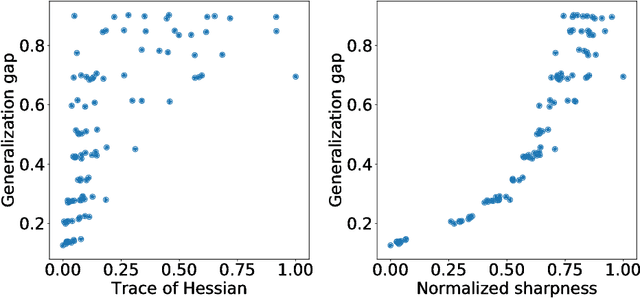


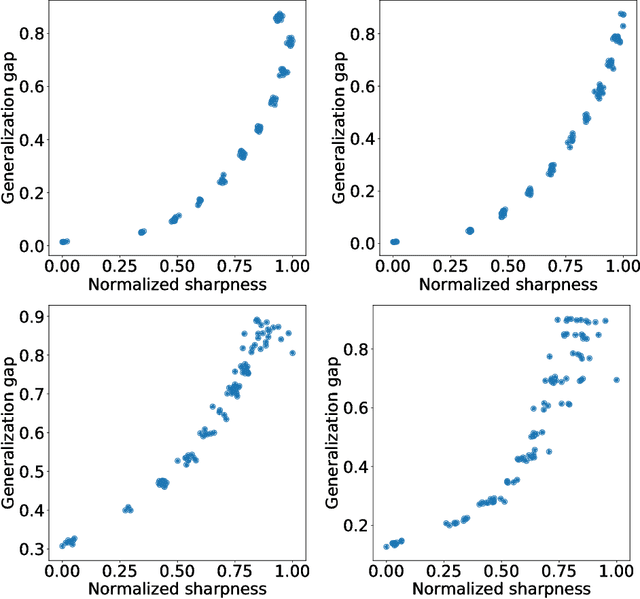
The notion of flat minima has played a key role in the generalization studies of deep learning models. However, existing definitions of the flatness are known to be sensitive to the rescaling of parameters. The issue suggests that the previous definitions of the flatness might not be a good measure of generalization, because generalization is invariant to such rescalings. In this paper, from the PAC-Bayesian perspective, we scrutinize the discussion concerning the flat minima and introduce the notion of normalized flat minima, which is free from the known scale dependence issues. Additionally, we highlight the scale dependence of existing matrix-norm based generalization error bounds similar to the existing flat minima definitions. Our modified notion of the flatness does not suffer from the insufficiency, either, suggesting it might provide better hierarchy in the hypothesis class.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge