Lipschitz-Margin Training: Scalable Certification of Perturbation Invariance for Deep Neural Networks
Paper and Code
Oct 31, 2018
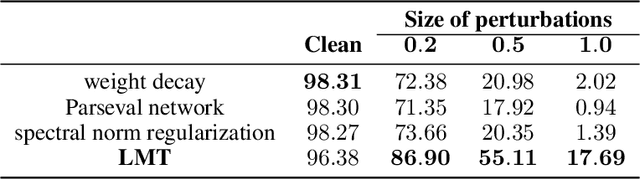

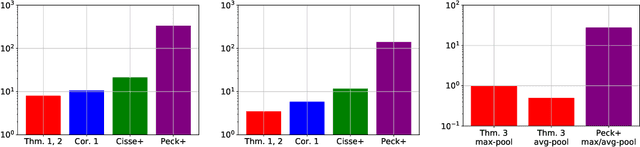
High sensitivity of neural networks against malicious perturbations on inputs causes security concerns. To take a steady step towards robust classifiers, we aim to create neural network models provably defended from perturbations. Prior certification work requires strong assumptions on network structures and massive computational costs, and thus the range of their applications was limited. From the relationship between the Lipschitz constants and prediction margins, we present a computationally efficient calculation technique to lower-bound the size of adversarial perturbations that can deceive networks, and that is widely applicable to various complicated networks. Moreover, we propose an efficient training procedure that robustifies networks and significantly improves the provably guarded areas around data points. In experimental evaluations, our method showed its ability to provide a non-trivial guarantee and enhance robustness for even large networks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge