Yurui Cao
Reinforcement Learning based Disease Progression Model for Alzheimer's Disease
Jun 30, 2021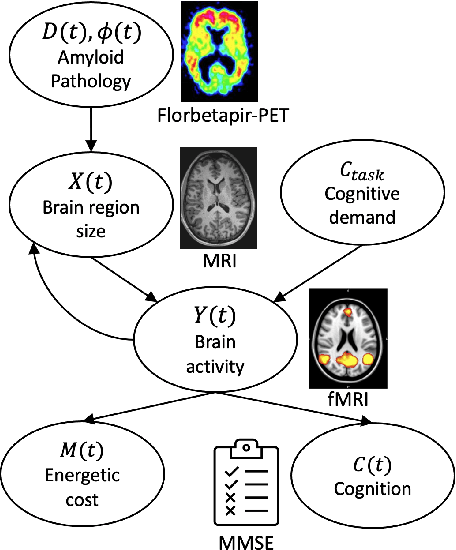
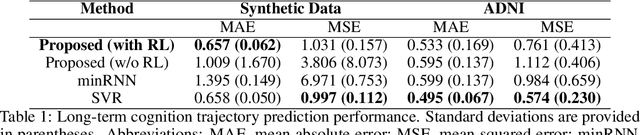
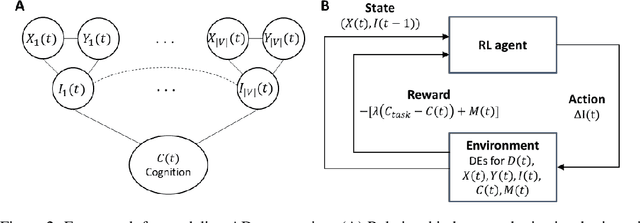
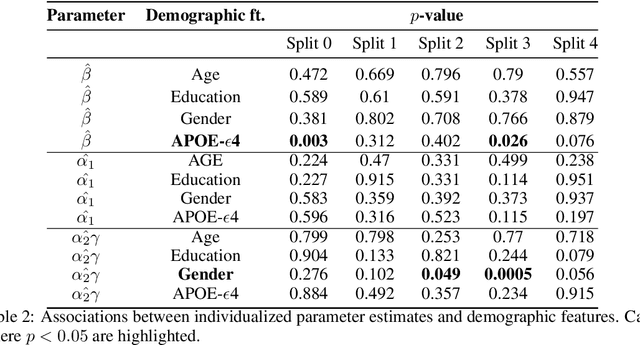
Abstract:We model Alzheimer's disease (AD) progression by combining differential equations (DEs) and reinforcement learning (RL) with domain knowledge. DEs provide relationships between some, but not all, factors relevant to AD. We assume that the missing relationships must satisfy general criteria about the working of the brain, for e.g., maximizing cognition while minimizing the cost of supporting cognition. This allows us to extract the missing relationships by using RL to optimize an objective (reward) function that captures the above criteria. We use our model consisting of DEs (as a simulator) and the trained RL agent to predict individualized 10-year AD progression using baseline (year 0) features on synthetic and real data. The model was comparable or better at predicting 10-year cognition trajectories than state-of-the-art learning-based models. Our interpretable model demonstrated, and provided insights into, "recovery/compensatory" processes that mitigate the effect of AD, even though those processes were not explicitly encoded in the model. Our framework combines DEs with RL for modelling AD progression and has broad applicability for understanding other neurological disorders.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge