Exploring the Performance Improvement of Tensor Processing Engines through Transformation in the Bit-weight Dimension of MACs

General matrix-matrix multiplication (GEMM) is a cornerstone of AI computations, making tensor processing engines (TPEs) increasingly critical in GPUs and domain-specific architectures. Existing architectures primarily optimize dataflow or operand reuse strategies. However, considering the interaction between matrix multiplication and multiply-accumulators (MACs) offers greater optimization potential. This work introduces a novel hardware perspective on matrix multiplication, focusing on the bit-weight dimension of MACs. We propose a finer-grained TPE notation using matrix triple loops as an example, introducing new methods for designing and optimizing PE microarchitectures. Based on this notation and its transformations, we propose four optimization techniques that improve timing, area, and power consumption. Implementing our design in RTL using the SMIC-28nm process, we evaluate its effectiveness across four classic TPE architectures: systolic array, 3D-Cube, multiplier-adder tree, and 2D-Matrix. Our techniques achieve area efficiency improvements of 1.27x, 1.28x, 1.56x, and 1.44x, and energy efficiency gains of 1.04x, 1.56x, 1.49x, and 1.20x, respectively. Applied to a bit-slice architecture, our approach achieves a 12.10x improvement in energy efficiency and 2.85x in area efficiency compared to Laconic. Our Verilog HDL code, along with timing, area, and power reports, is available at https://github.com/wqzustc/High-Performance-Tensor-Processing-Engines

Efficient Message Passing Architecture for GCN Training on HBM-based FPGAs with Orthogonal Topology On-Chip Networks

Graph Convolutional Networks (GCNs) are state-of-the-art deep learning models for representation learning on graphs. However, the efficient training of GCNs is hampered by constraints in memory capacity and bandwidth, compounded by the irregular data flow that results in communication bottlenecks. To address these challenges, we propose a message-passing architecture that leverages NUMA-based memory access properties and employs a parallel multicast routing algorithm based on a 4-D hypercube network within the accelerator for efficient message passing in graphs. Additionally, we have re-engineered the backpropagation algorithm specific to GCNs within our proposed accelerator. This redesign strategically mitigates the memory demands prevalent during the training phase and diminishes the computational overhead associated with the transposition of extensive matrices. Compared to the state-of-the-art HP-GNN architecture we achieved a performance improvement of $1.03\times \sim 1.81\times$.

Hardware Acceleration of Sampling Algorithms in Sample and Aggregate Graph Neural Networks

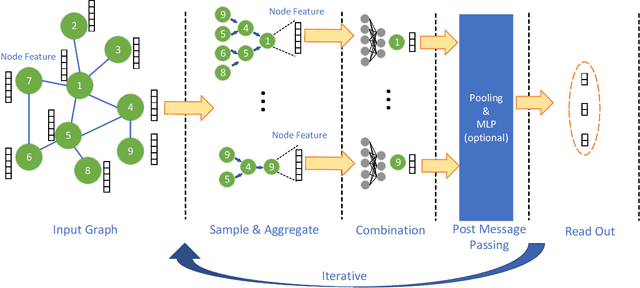
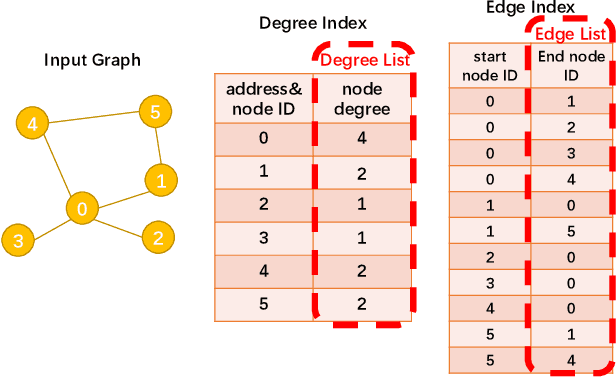
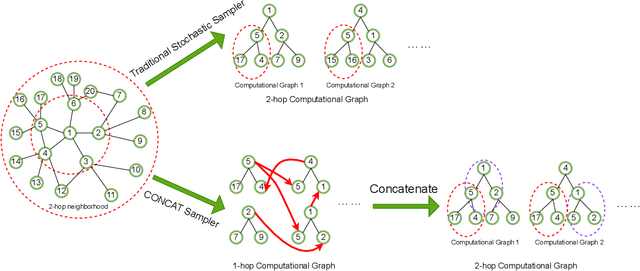
Sampling is an important process in many GNN structures in order to train larger datasets with a smaller computational complexity. However, compared to other processes in GNN (such as aggregate, backward propagation), the sampling process still costs tremendous time, which limits the speed of training. To reduce the time of sampling, hardware acceleration is an ideal choice. However, state of the art GNN acceleration proposal did not specify how to accelerate the sampling process. What's more, directly accelerating traditional sampling algorithms will make the structure of the accelerator very complicated. In this work, we made two contributions: (1) Proposed a new neighbor sampler: CONCAT Sampler, which can be easily accelerated on hardware level while guaranteeing the test accuracy. (2) Designed a CONCAT-sampler-accelerator based on FPGA, with which the neighbor sampling process boosted to about 300-1000 times faster compared to the sampling process without it.