An Interval Branch-and-Bound-Based Inverse Kinemetics Algorithm Towards Global Optimal Redundancy Resolution

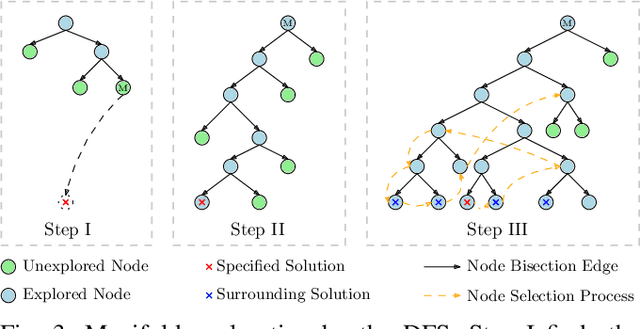
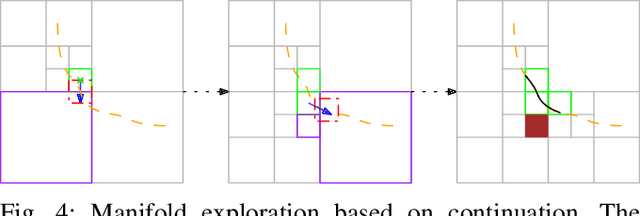
The general inverse kinematics (IK) problem of a manipulator, namely that of acquiring the self-motion manifold (SMM) of all admissible joint angles for a desired end-effector pose, plays a vital role in robotics modeling, planning and control. To efficiently solve the generalized IK, this paper proposes an interval branch-and-bound-based approach, which is augmented with a fast numerical IK-solver-enabled search heuristics. In comparison to independent solutions generated by sampling based methods, our approach generates patches of neighboring solutions to provide richer information of the inherent geometry of the SMM for optimal planning and other applications. It can also be utilized in an anytime fashion to obtain solutions with sub-optimal resolution for applications within a limited period. The performance of our approach is verified by numerical experiments on both non-redundant and redundant manipulators.

A Novel GPU-based Parallel Implementation Scheme and Performance Analysis of Robot Forward Dynamics Algorithms

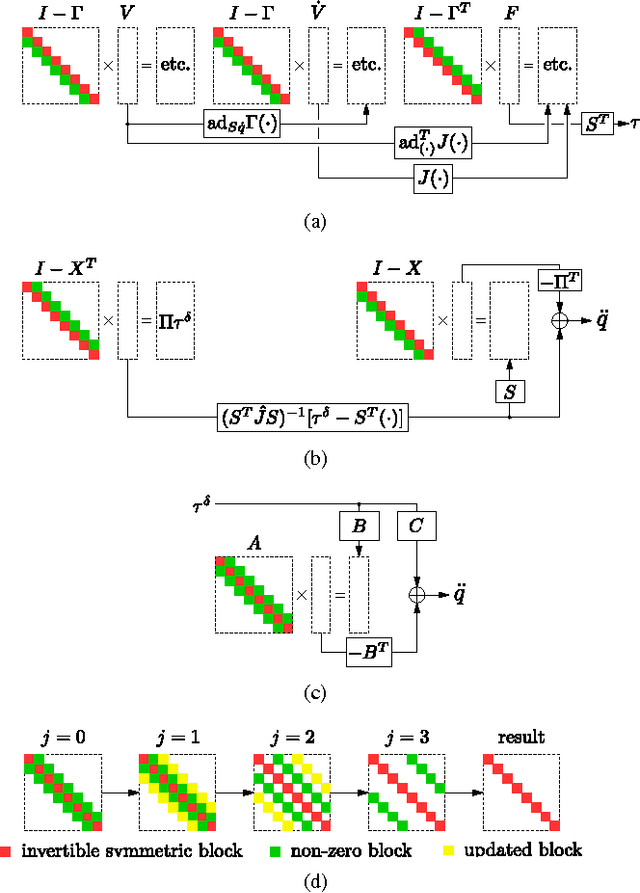
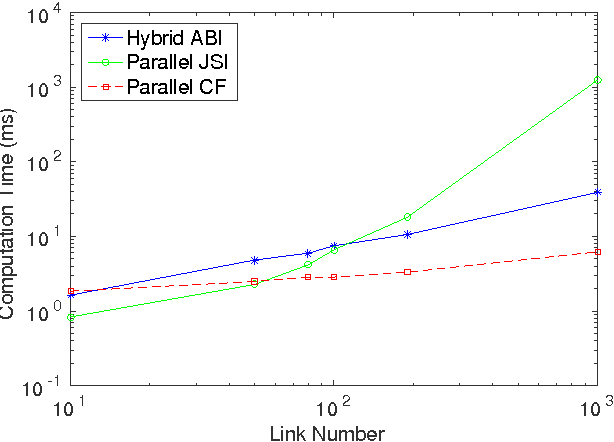
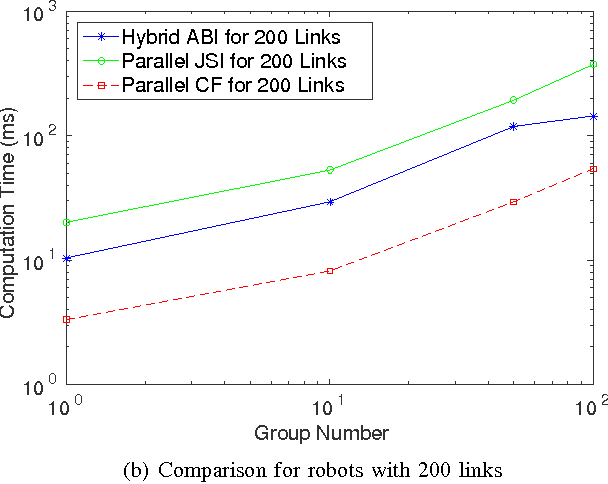
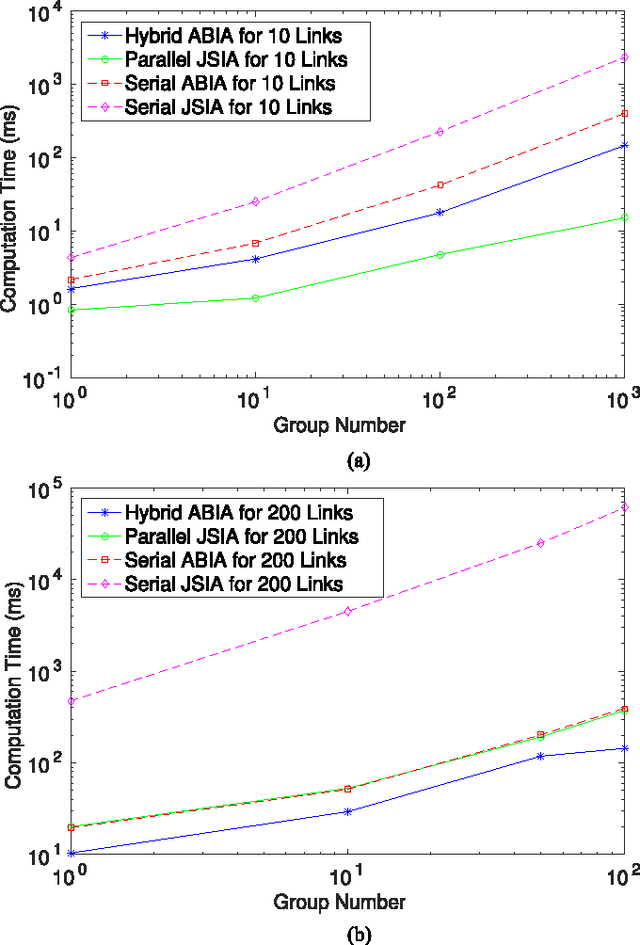
We propose a novel unifying scheme for parallel implementation of articulated robot dynamics algorithms. It is based on a unified Lie group notation for deriving the equations of motion of articulated robots, where various well-known forward algorithms differ only by their joint inertia matrix inversion strategies. This new scheme leads to a unified abstraction of state-of-the-art forward dynamics algorithms into combinations of block bi-diagonal and/or block tri-diagonal systems, which may be efficiently solved by parallel all-prefix-sum operations (scan) and parallel odd-even elimination (OEE) respectively. We implement the proposed scheme on a Nvidia CUDA GPU platform for the comparative study of three algorithms, namely the hybrid articulated-body inertia algorithm (ABIA), the parallel joint space inertia inversion algorithm (JSIIA) and the constrained force algorithm (CFA), and the performances are analyzed.

Parallel Dynamics Computation using Prefix Sum Operations

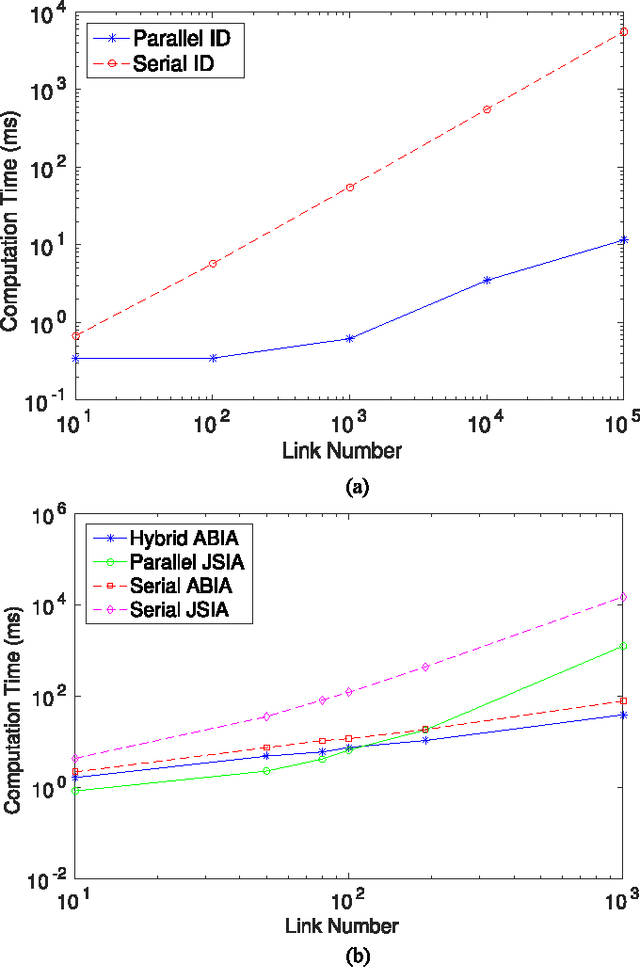
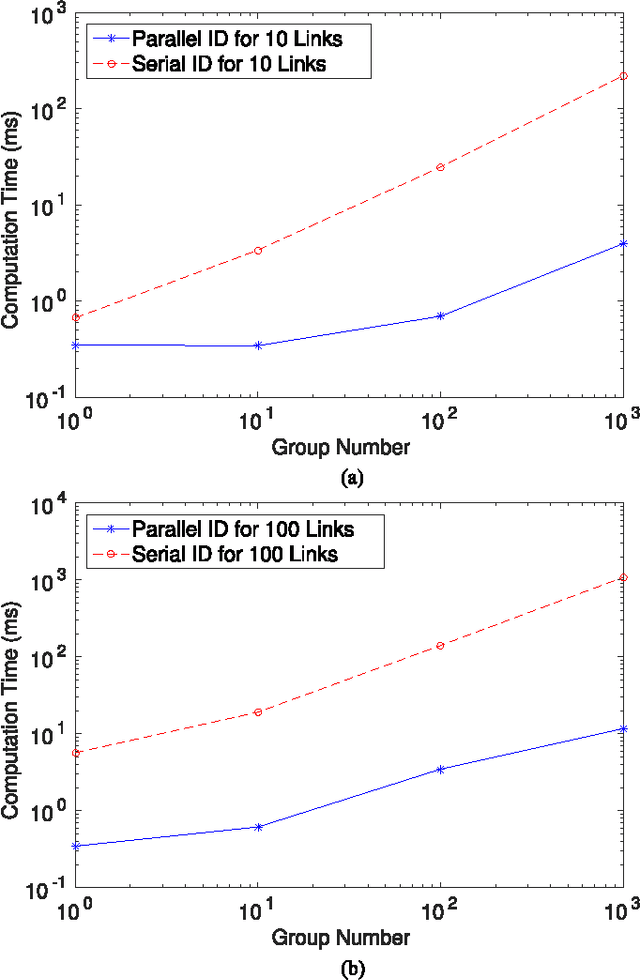
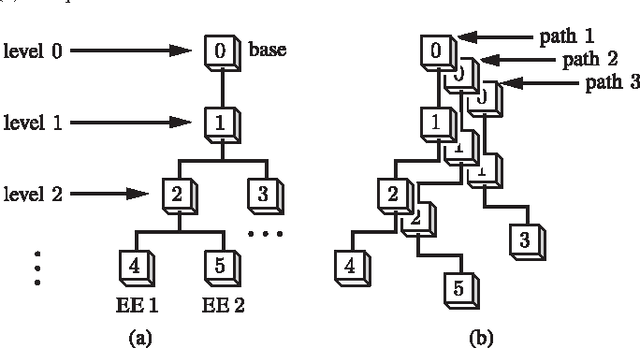
We propose a new parallel framework for fast computation of inverse and forward dynamics of articulated robots based on prefix sums (scans). We re-investigate the well-known recursive Newton-Euler formulation of robot dynamics and show that the forward-backward propagation process for robot inverse dynamics is equivalent to two scan operations on certain semigroups. We show that the state-of-the-art forward dynamics algorithms may almost completely be cast into a sequence of scan operations, with unscannable parts clearly identified. This suggests a serial-parallel hybrid approach for systems with a moderate number of links. We implement our scan based algorithms on Nvidia CUDA platform with performance compared with multithreading CPU-based recursive algorithms; a significant level of acceleration is demonstrated.