Parallel Dynamics Computation using Prefix Sum Operations
Paper and Code
Sep 15, 2016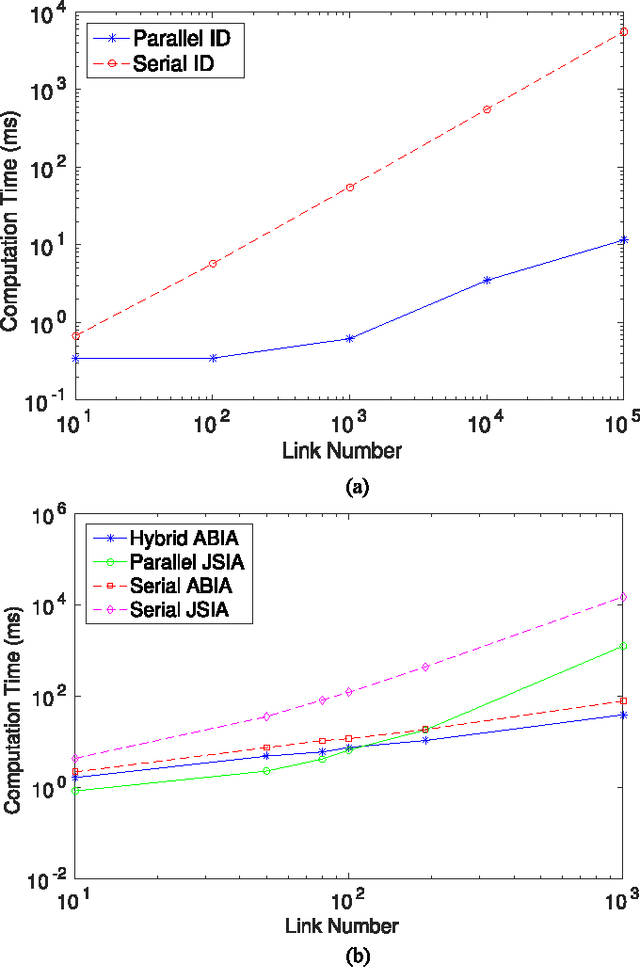
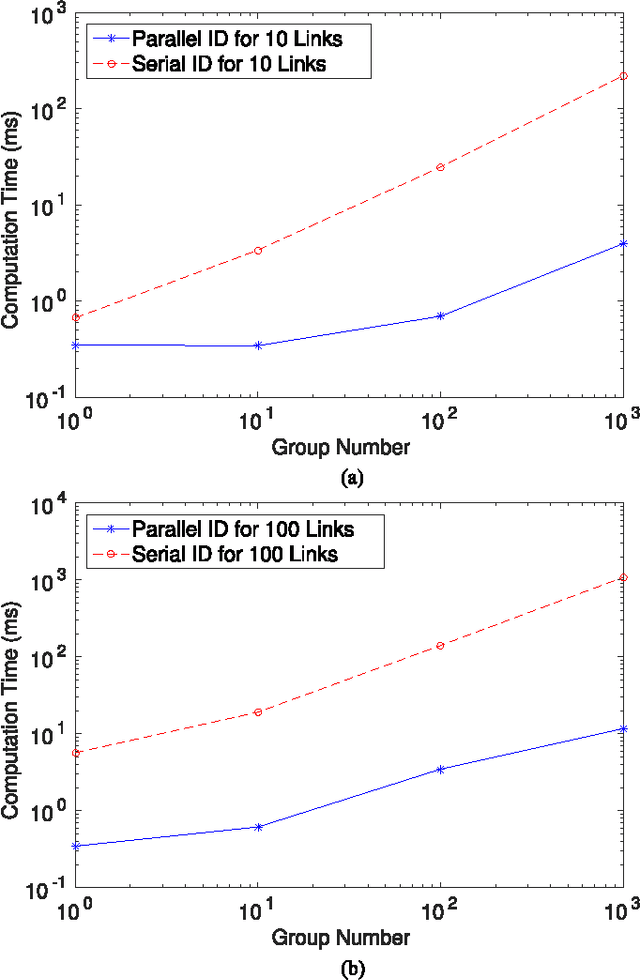
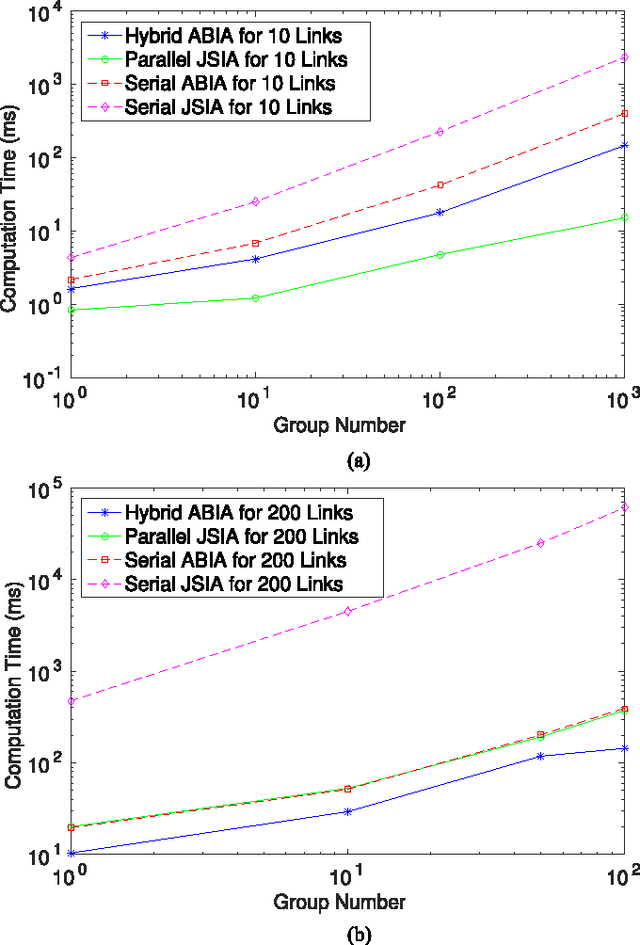
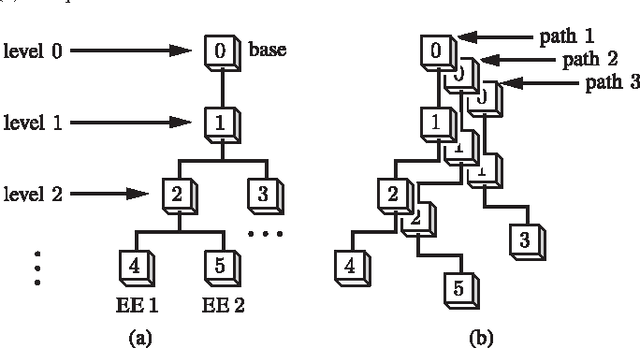
We propose a new parallel framework for fast computation of inverse and forward dynamics of articulated robots based on prefix sums (scans). We re-investigate the well-known recursive Newton-Euler formulation of robot dynamics and show that the forward-backward propagation process for robot inverse dynamics is equivalent to two scan operations on certain semigroups. We show that the state-of-the-art forward dynamics algorithms may almost completely be cast into a sequence of scan operations, with unscannable parts clearly identified. This suggests a serial-parallel hybrid approach for systems with a moderate number of links. We implement our scan based algorithms on Nvidia CUDA platform with performance compared with multithreading CPU-based recursive algorithms; a significant level of acceleration is demonstrated.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge