An Interval Branch-and-Bound-Based Inverse Kinemetics Algorithm Towards Global Optimal Redundancy Resolution
Paper and Code
Apr 25, 2021

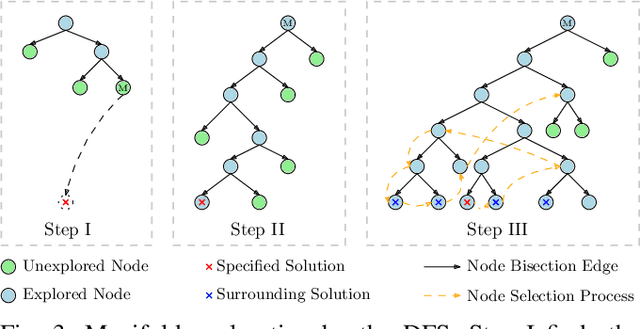
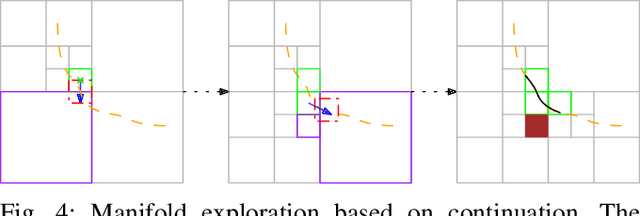
The general inverse kinematics (IK) problem of a manipulator, namely that of acquiring the self-motion manifold (SMM) of all admissible joint angles for a desired end-effector pose, plays a vital role in robotics modeling, planning and control. To efficiently solve the generalized IK, this paper proposes an interval branch-and-bound-based approach, which is augmented with a fast numerical IK-solver-enabled search heuristics. In comparison to independent solutions generated by sampling based methods, our approach generates patches of neighboring solutions to provide richer information of the inherent geometry of the SMM for optimal planning and other applications. It can also be utilized in an anytime fashion to obtain solutions with sub-optimal resolution for applications within a limited period. The performance of our approach is verified by numerical experiments on both non-redundant and redundant manipulators.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge