Fine-Grained System Identification of Nonlinear Neural Circuits

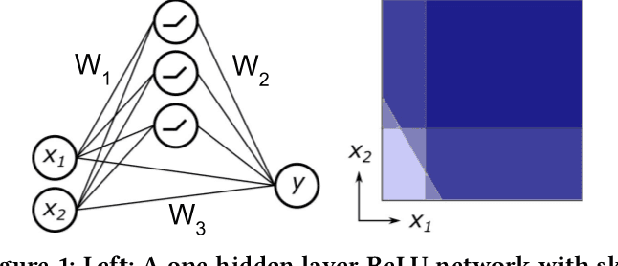
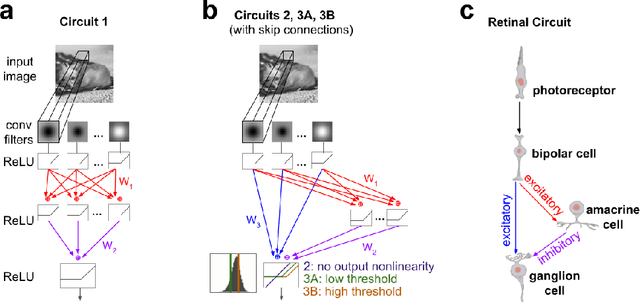
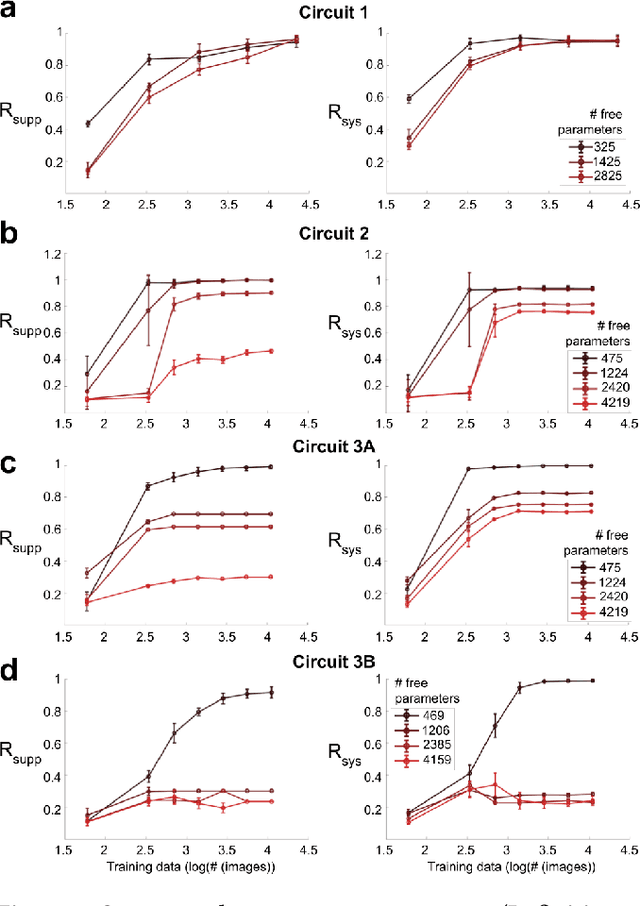
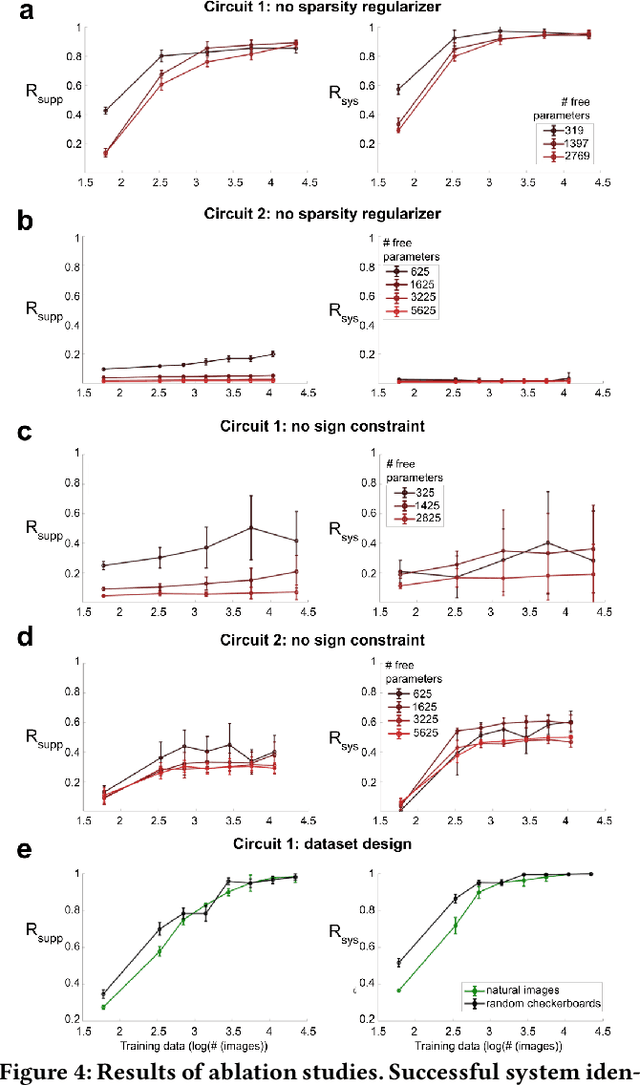
We study the problem of sparse nonlinear model recovery of high dimensional compositional functions. Our study is motivated by emerging opportunities in neuroscience to recover fine-grained models of biological neural circuits using collected measurement data. Guided by available domain knowledge in neuroscience, we explore conditions under which one can recover the underlying biological circuit that generated the training data. Our results suggest insights of both theoretical and practical interests. Most notably, we find that a sign constraint on the weights is a necessary condition for system recovery, which we establish both theoretically with an identifiability guarantee and empirically on simulated biological circuits. We conclude with a case study on retinal ganglion cell circuits using data collected from mouse retina, showcasing the practical potential of this approach.

condLSTM-Q: A novel deep learning model for predicting Covid-19 mortality in fine geographical Scale

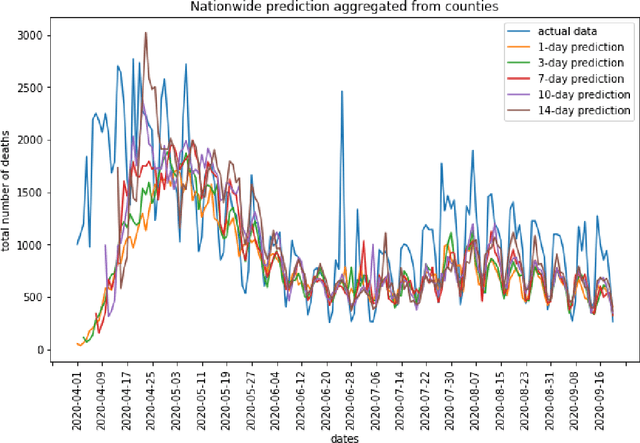
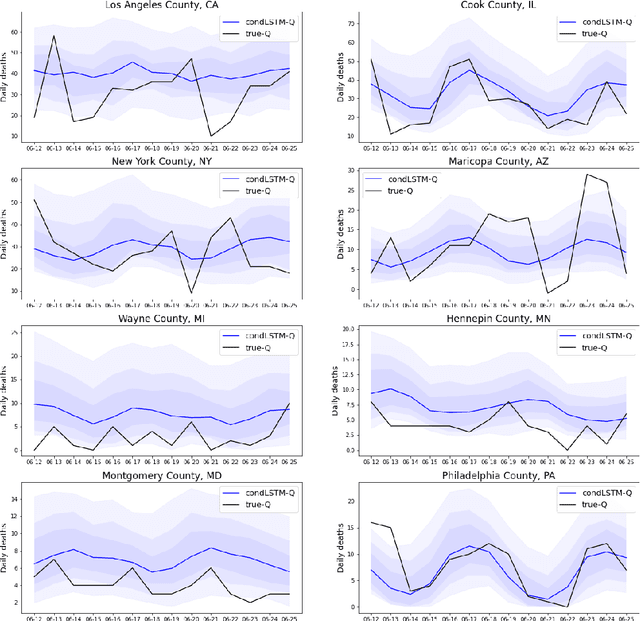
Predictive models with a focus on different spatial-temporal scales benefit governments and healthcare systems to combat the COVID-19 pandemic. Here we present the conditional Long Short-Term Memory networks with Quantile output (condLSTM-Q), a well-performing model for making quantile predictions on COVID-19 death tolls at the county level with a two-week forecast window. This fine geographical scale is a rare but useful feature in publicly available predictive models, which would especially benefit state-level officials to coordinate resources within the state. The quantile predictions from condLSTM-Q inform people about the distribution of the predicted death tolls, allowing better evaluation of possible trajectories of the severity. Given the scalability and generalizability of neural network models, this model could incorporate additional data sources with ease, and could be further developed to generate other useful predictions such as new cases or hospitalizations intuitively.