Covariance Matrix Adaptation Evolutionary Strategy with Worst-Case Ranking Approximation for Min--Max Optimization and its Application to Berthing Control Tasks

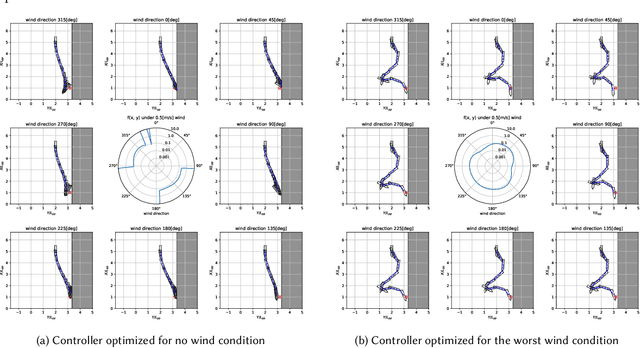
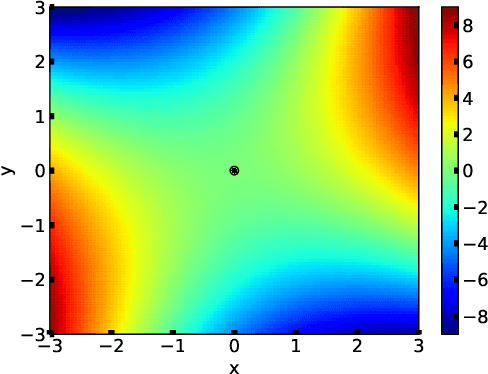
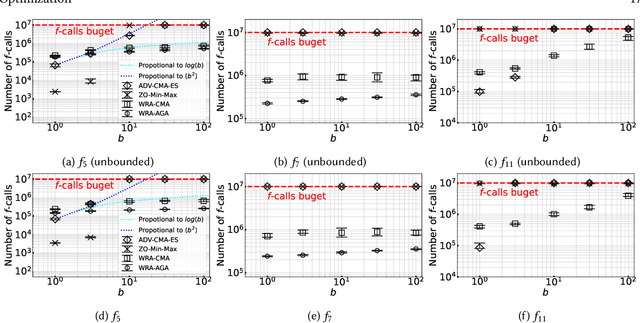
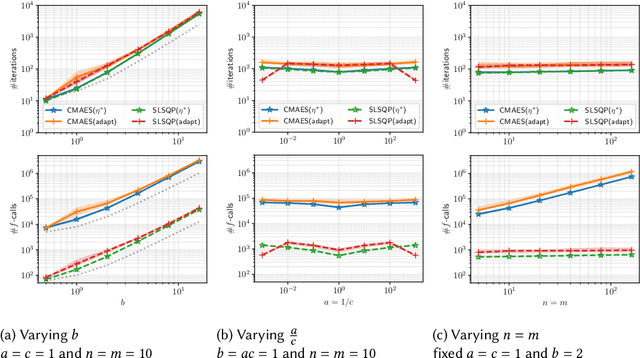
In this study, we consider a continuous min--max optimization problem $\min_{x \in \mathbb{X} \max_{y \in \mathbb{Y}}}f(x,y)$ whose objective function is a black-box. We propose a novel approach to minimize the worst-case objective function $F(x) = \max_{y} f(x,y)$ directly using a covariance matrix adaptation evolution strategy (CMA-ES) in which the rankings of solution candidates are approximated by our proposed worst-case ranking approximation (WRA) mechanism. We develop two variants of WRA combined with CMA-ES and approximate gradient ascent as numerical solvers for the inner maximization problem. Numerical experiments show that our proposed approach outperforms several existing approaches when the objective function is a smooth strongly convex--concave function and the interaction between $x$ and $y$ is strong. We investigate the advantages of the proposed approach for problems where the objective function is not limited to smooth strongly convex--concave functions. The effectiveness of the proposed approach is demonstrated in the robust berthing control problem with uncertainty.ngly convex--concave functions. The effectiveness of the proposed approach is demonstrated in the robust berthing control problem with uncertainty.

Ship trajectory planning method for reproducing human operation at ports

Among ship maneuvers, berthing/unberthing maneuvers are one of the most challenging and stressful phases for captains. Concerning burden reduction on ship operators and preventing accidents, several researches have been conducted on trajectory planning to automate berthing/unberthing. However, few studies have aimed at assisting captains in berthing/unberthing. The trajectory to be presented to the captain should be a maneuver that reproduces human captain's control characteristics. The previously proposed methods cannot explicitly reflect the motion and navigation, which human captains pay particular attention to reduce the mental burden in the trajectory planning. Herein, mild constraints to the trajectory planning method are introduced. The constraints impose certain states (position, bow heading angle, ship speed, and yaw angular velocity), to be taken approximately at any given time. The introduction of this new constraint allows imposing careful trajectory planning (e.g., in-situ turns at zero speed or a pause for safety before going astern), as if performed by a human during berthing/unberthing. The algorithm proposed herein was used to optimize the berthing/unberthing trajectories for a large car ferry. The results show that this method can generate the quantitatively equivalent trajectory recorded in the actual berthing/unberthing maneuver performed by a human captain.

Collision probability reduction method for tracking control in automatic docking / berthing using reinforcement learning

Automation of berthing maneuvers in shipping is a pressing issue as the berthing maneuver is one of the most stressful tasks seafarers undertake. Berthing control problems are often tackled via tracking a predefined trajectory or path. Maintaining a tracking error of zero under an uncertain environment is impossible; the tracking controller is nonetheless required to bring vessels close to desired berths. The tracking controller must prioritize the avoidance of tracking errors that may cause collisions with obstacles. This paper proposes a training method based on reinforcement learning for a trajectory tracking controller that reduces the probability of collisions with static obstacles. Via numerical simulations, we show that the proposed method reduces the probability of collisions during berthing maneuvers. Furthermore, this paper shows the tracking performance in a model experiment.

Saddle Point Optimization with Approximate Minimization Oracle and its Application to Robust Berthing Control

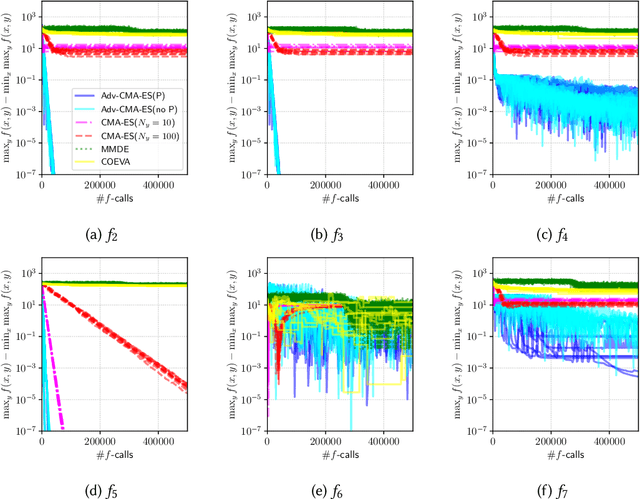
We propose an approach to saddle point optimization relying only on an oracle that solves a minimization problem approximately. We analyze its convergence property on a strongly convex--concave problem and show its linear convergence toward the global min--max saddle point. Based on the convergence analysis, we propose a heuristic approach to adapt the learning rate for the proposed saddle point optimization approach. The implementation of the proposed approach using the (1+1)-CMA-ES as the minimization oracle, namely Adversarial-CMA-ES, is evaluated on test problems. Numerical evaluation reveals the tightness of the theoretical convergence rate bound as well as the efficiency of the learning rate adaptation mechanism. As an example of real-world applications, it is applied to automatic berthing control problems under model uncertainties, showing its usefulness in obtaining solutions robust under model uncertainties.