Covariance Matrix Adaptation Evolutionary Strategy with Worst-Case Ranking Approximation for Min--Max Optimization and its Application to Berthing Control Tasks
Paper and Code
Mar 28, 2023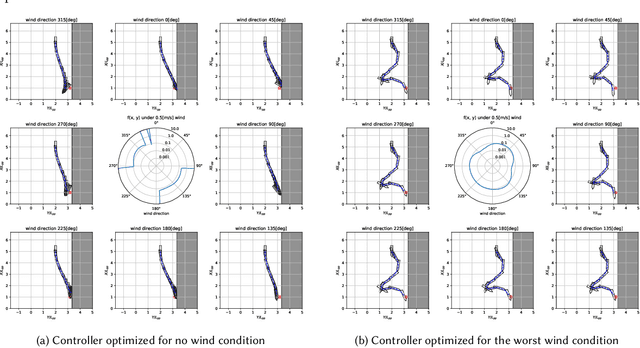

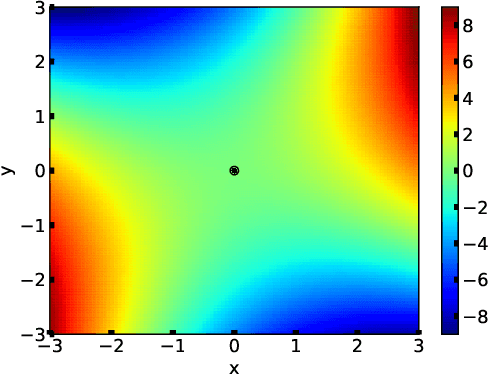
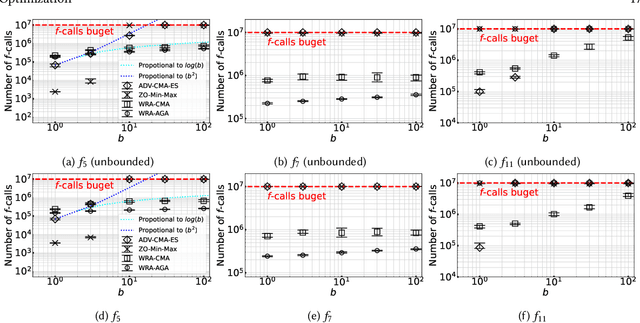
In this study, we consider a continuous min--max optimization problem $\min_{x \in \mathbb{X} \max_{y \in \mathbb{Y}}}f(x,y)$ whose objective function is a black-box. We propose a novel approach to minimize the worst-case objective function $F(x) = \max_{y} f(x,y)$ directly using a covariance matrix adaptation evolution strategy (CMA-ES) in which the rankings of solution candidates are approximated by our proposed worst-case ranking approximation (WRA) mechanism. We develop two variants of WRA combined with CMA-ES and approximate gradient ascent as numerical solvers for the inner maximization problem. Numerical experiments show that our proposed approach outperforms several existing approaches when the objective function is a smooth strongly convex--concave function and the interaction between $x$ and $y$ is strong. We investigate the advantages of the proposed approach for problems where the objective function is not limited to smooth strongly convex--concave functions. The effectiveness of the proposed approach is demonstrated in the robust berthing control problem with uncertainty.ngly convex--concave functions. The effectiveness of the proposed approach is demonstrated in the robust berthing control problem with uncertainty.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge