Covariance Matrix Adaptation Evolutionary Strategy with Worst-Case Ranking Approximation for Min--Max Optimization and its Application to Berthing Control Tasks

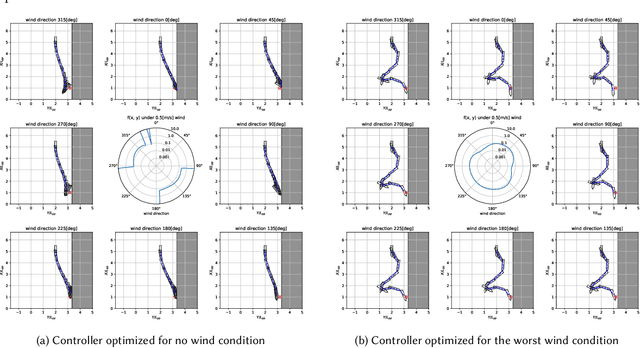
In this study, we consider a continuous min--max optimization problem $\min_{x \in \mathbb{X} \max_{y \in \mathbb{Y}}}f(x,y)$ whose objective function is a black-box. We propose a novel approach to minimize the worst-case objective function $F(x) = \max_{y} f(x,y)$ directly using a covariance matrix adaptation evolution strategy (CMA-ES) in which the rankings of solution candidates are approximated by our proposed worst-case ranking approximation (WRA) mechanism. We develop two variants of WRA combined with CMA-ES and approximate gradient ascent as numerical solvers for the inner maximization problem. Numerical experiments show that our proposed approach outperforms several existing approaches when the objective function is a smooth strongly convex--concave function and the interaction between $x$ and $y$ is strong. We investigate the advantages of the proposed approach for problems where the objective function is not limited to smooth strongly convex--concave functions. The effectiveness of the proposed approach is demonstrated in the robust berthing control problem with uncertainty.ngly convex--concave functions. The effectiveness of the proposed approach is demonstrated in the robust berthing control problem with uncertainty.

Adaptive Scenario Subset Selection for Worst-Case Optimization and its Application to Well Placement Optimization

In this study, we consider simulation-based worst-case optimization problems with continuous design variables and a finite scenario set. To reduce the number of simulations required and increase the number of restarts for better local optimum solutions, we propose a new approach referred to as adaptive scenario subset selection (AS3). The proposed approach subsamples a scenario subset as a support to construct the worst-case function in a given neighborhood, and we introduce such a scenario subset. Moreover, we develop a new optimization algorithm by combining AS3 and the covariance matrix adaptation evolution strategy (CMA-ES), denoted AS3-CMA-ES. At each algorithmic iteration, a subset of support scenarios is selected, and CMA-ES attempts to optimize the worst-case objective computed only through a subset of the scenarios. The proposed algorithm reduces the number of simulations required by executing simulations on only a scenario subset, rather than on all scenarios. In numerical experiments, we verified that AS3-CMA-ES is more efficient in terms of the number of simulations than the brute-force approach and a surrogate-assisted approach lq-CMA-ES when the ratio of the number of support scenarios to the total number of scenarios is relatively small. In addition, the usefulness of AS3-CMA-ES was evaluated for well placement optimization for carbon dioxide capture and storage (CCS). In comparison with the brute-force approach and lq-CMA-ES, AS3-CMA-ES was able to find better solutions because of more frequent restarts.

Black-Box Min--Max Continuous Optimization Using CMA-ES with Worst-case Ranking Approximation

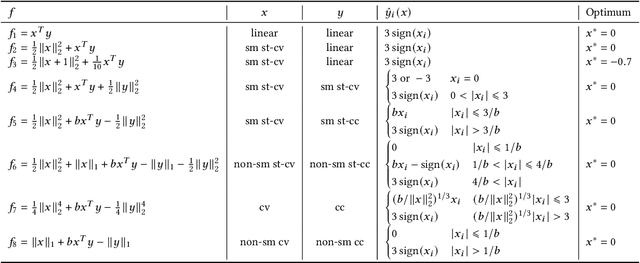
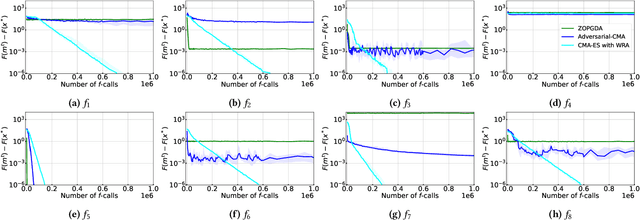
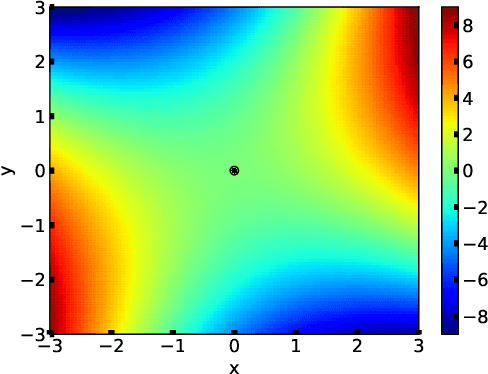
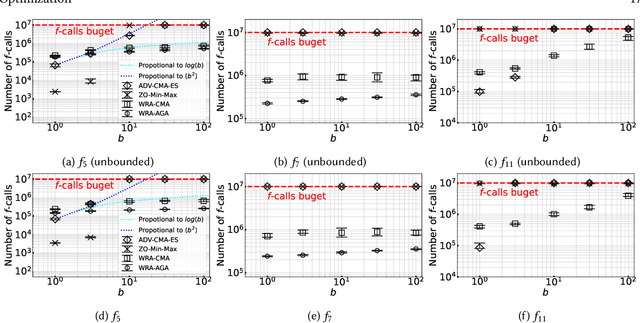
In this study, we investigate the problem of min-max continuous optimization in a black-box setting $\min_{x} \max_{y}f(x,y)$. A popular approach updates $x$ and $y$ simultaneously or alternatingly. However, two major limitations have been reported in existing approaches. (I) As the influence of the interaction term between $x$ and $y$ (e.g., $x^\mathrm{T} B y$) on the Lipschitz smooth and strongly convex-concave function $f$ increases, the approaches converge to an optimal solution at a slower rate. (II) The approaches fail to converge if $f$ is not Lipschitz smooth and strongly convex-concave around the optimal solution. To address these difficulties, we propose minimizing the worst-case objective function $F(x)=\max_{y}f(x,y)$ directly using the covariance matrix adaptation evolution strategy, in which the rankings of solution candidates are approximated by our proposed worst-case ranking approximation (WRA) mechanism. Compared with existing approaches, numerical experiments show two important findings regarding our proposed method. (1) The proposed approach is efficient in terms of $f$-calls on a Lipschitz smooth and strongly convex-concave function with a large interaction term. (2) The proposed approach can converge on functions that are not Lipschitz smooth and strongly convex-concave around the optimal solution, whereas existing approaches fail.