Saddle Point Optimization with Approximate Minimization Oracle and its Application to Robust Berthing Control
Paper and Code
May 26, 2021

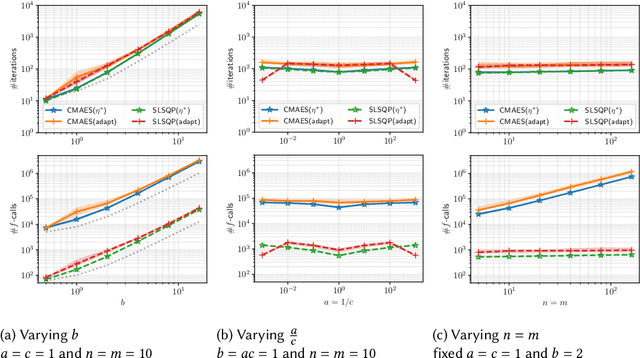
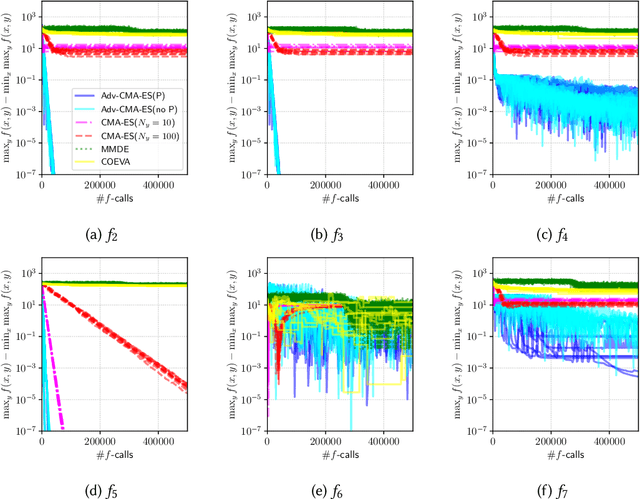
We propose an approach to saddle point optimization relying only on an oracle that solves a minimization problem approximately. We analyze its convergence property on a strongly convex--concave problem and show its linear convergence toward the global min--max saddle point. Based on the convergence analysis, we propose a heuristic approach to adapt the learning rate for the proposed saddle point optimization approach. The implementation of the proposed approach using the (1+1)-CMA-ES as the minimization oracle, namely Adversarial-CMA-ES, is evaluated on test problems. Numerical evaluation reveals the tightness of the theoretical convergence rate bound as well as the efficiency of the learning rate adaptation mechanism. As an example of real-world applications, it is applied to automatic berthing control problems under model uncertainties, showing its usefulness in obtaining solutions robust under model uncertainties.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge