Stochastic Precision Ensemble: Self-Knowledge Distillation for Quantized Deep Neural Networks

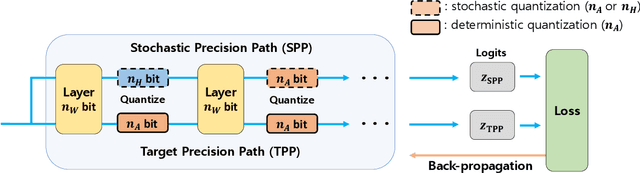
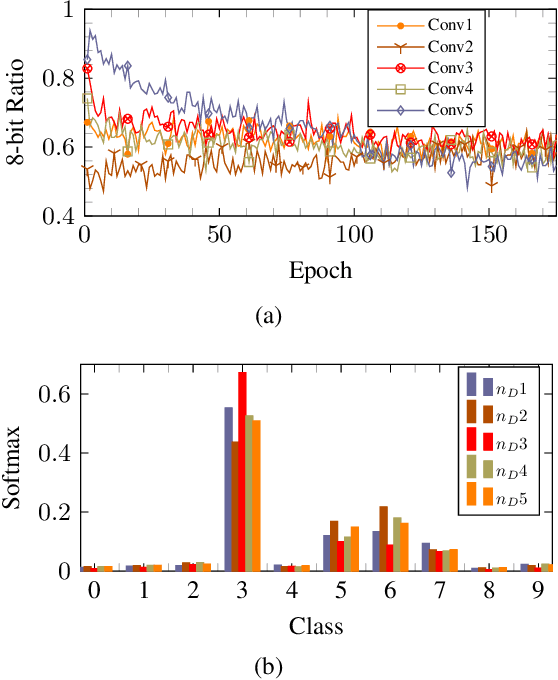
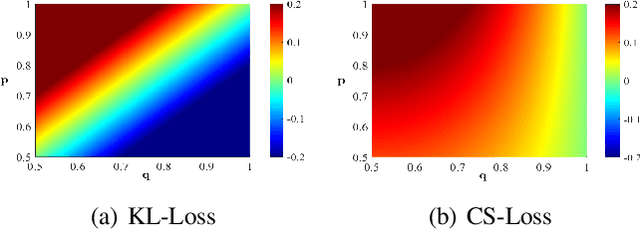
The quantization of deep neural networks (QDNNs) has been actively studied for deployment in edge devices. Recent studies employ the knowledge distillation (KD) method to improve the performance of quantized networks. In this study, we propose stochastic precision ensemble training for QDNNs (SPEQ). SPEQ is a knowledge distillation training scheme; however, the teacher is formed by sharing the model parameters of the student network. We obtain the soft labels of the teacher by changing the bit precision of the activation stochastically at each layer of the forward-pass computation. The student model is trained with these soft labels to reduce the activation quantization noise. The cosine similarity loss is employed, instead of the KL-divergence, for KD training. As the teacher model changes continuously by random bit-precision assignment, it exploits the effect of stochastic ensemble KD. SPEQ outperforms the existing quantization training methods in various tasks, such as image classification, question-answering, and transfer learning without the need for cumbersome teacher networks.

Quantized Neural Networks: Characterization and Holistic Optimization

Quantized deep neural networks (QDNNs) are necessary for low-power, high throughput, and embedded applications. Previous studies mostly focused on developing optimization methods for the quantization of given models. However, quantization sensitivity depends on the model architecture. Therefore, the model selection needs to be a part of the QDNN design process. Also, the characteristics of weight and activation quantization are quite different. This study proposes a holistic approach for the optimization of QDNNs, which contains QDNN training methods as well as quantization-friendly architecture design. Synthesized data is used to visualize the effects of weight and activation quantization. The results indicate that deeper models are more prone to activation quantization, while wider models improve the resiliency to both weight and activation quantization. This study can provide insight into better optimization of QDNNs.

SQWA: Stochastic Quantized Weight Averaging for Improving the Generalization Capability of Low-Precision Deep Neural Networks

Designing a deep neural network (DNN) with good generalization capability is a complex process especially when the weights are severely quantized. Model averaging is a promising approach for achieving the good generalization capability of DNNs, especially when the loss surface for training contains many sharp minima. We present a new quantized neural network optimization approach, stochastic quantized weight averaging (SQWA), to design low-precision DNNs with good generalization capability using model averaging. The proposed approach includes (1) floating-point model training, (2) direct quantization of weights, (3) capturing multiple low-precision models during retraining with cyclical learning rates, (4) averaging the captured models, and (5) re-quantizing the averaged model and fine-tuning it with low-learning rates. Additionally, we present a loss-visualization technique on the quantized weight domain to clearly elucidate the behavior of the proposed method. Visualization results indicate that a quantized DNN (QDNN) optimized with the proposed approach is located near the center of the flat minimum in the loss surface. With SQWA training, we achieved state-of-the-art results for 2-bit QDNNs on CIFAR-100 and ImageNet datasets. Although we only employed a uniform quantization scheme for the sake of implementation in VLSI or low-precision neural processing units, the performance achieved exceeded those of previous studies employing non-uniform quantization.

Empirical Analysis of Knowledge Distillation Technique for Optimization of Quantized Deep Neural Networks

Knowledge distillation (KD) is a very popular method for model size reduction. Recently, the technique is exploited for quantized deep neural networks (QDNNs) training as a way to restore the performance sacrificed by word-length reduction. KD, however, employs additional hyper-parameters, such as temperature, coefficient, and the size of teacher network for QDNN training. We analyze the effect of these hyper-parameters for QDNN optimization with KD. We find that these hyper-parameters are inter-related, and also introduce a simple and effective technique that reduces \textit{coefficient} during training. With KD employing the proposed hyper-parameters, we achieve the test accuracy of 92.7% and 67.0% on Resnet20 with 2-bit ternary weights for CIFAR-10 and CIFAR-100 data sets, respectively.

Structured Sparse Ternary Weight Coding of Deep Neural Networks for Efficient Hardware Implementations

Deep neural networks (DNNs) usually demand a large amount of operations for real-time inference. Especially, fully-connected layers contain a large number of weights, thus they usually need many off-chip memory accesses for inference. We propose a weight compression method for deep neural networks, which allows values of +1 or -1 only at predetermined positions of the weights so that decoding using a table can be conducted easily. For example, the structured sparse (8,2) coding allows at most two non-zero values among eight weights. This method not only enables multiplication-free DNN implementations but also compresses the weight storage by up to x32 compared to floating-point networks. Weight distribution normalization and gradual pruning techniques are applied to mitigate the performance degradation. The experiments are conducted with fully-connected deep neural networks and convolutional neural networks.

Fixed-point optimization of deep neural networks with adaptive step size retraining

Fixed-point optimization of deep neural networks plays an important role in hardware based design and low-power implementations. Many deep neural networks show fairly good performance even with 2- or 3-bit precision when quantized weights are fine-tuned by retraining. We propose an improved fixedpoint optimization algorithm that estimates the quantization step size dynamically during the retraining. In addition, a gradual quantization scheme is also tested, which sequentially applies fixed-point optimizations from high- to low-precision. The experiments are conducted for feed-forward deep neural networks (FFDNNs), convolutional neural networks (CNNs), and recurrent neural networks (RNNs).