Semi-supervised Learning with Deep Generative Models for Asset Failure Prediction

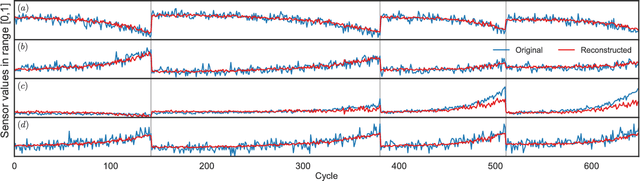
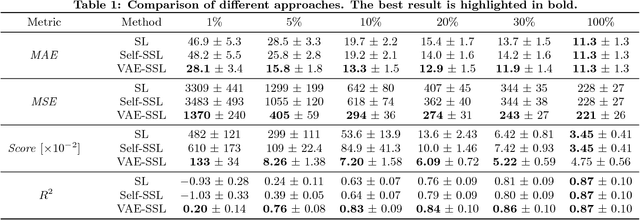
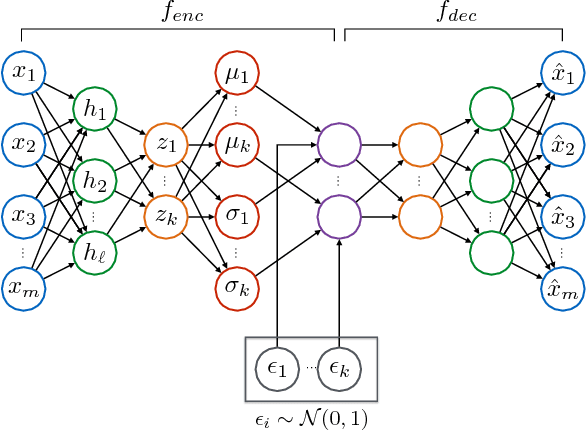
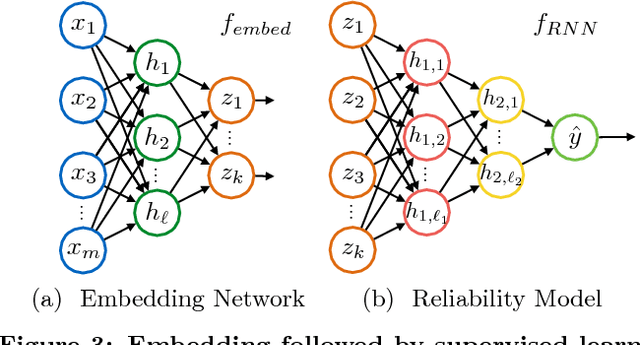
This work presents a novel semi-supervised learning approach for data-driven modeling of asset failures when health status is only partially known in historical data. We combine a generative model parameterized by deep neural networks with non-linear embedding technique. It allows us to build prognostic models with the limited amount of health status information for the precise prediction of future asset reliability. The proposed method is evaluated on a publicly available dataset for remaining useful life (RUL) estimation, which shows significant improvement even when a fraction of the data with known health status is as sparse as 1% of the total. Our study suggests that the non-linear embedding based on a deep generative model can efficiently regularize a complex model with deep architectures while achieving high prediction accuracy that is far less sensitive to the availability of health status information.

Efficient Energy Minimization for Enforcing Statistics

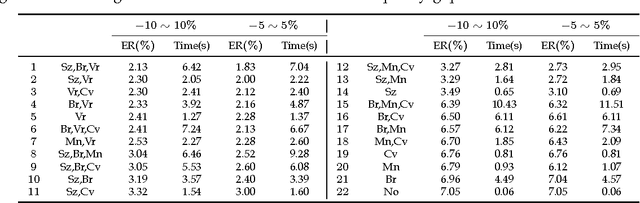
Energy minimization algorithms, such as graph cuts, enable the computation of the MAP solution under certain probabilistic models such as Markov random fields. However, for many computer vision problems, the MAP solution under the model is not the ground truth solution. In many problem scenarios, the system has access to certain statistics of the ground truth. For instance, in image segmentation, the area and boundary length of the object may be known. In these cases, we want to estimate the most probable solution that is consistent with such statistics, i.e., satisfies certain equality or inequality constraints. The above constrained energy minimization problem is NP-hard in general, and is usually solved using Linear Programming formulations, which relax the integrality constraints. This paper proposes a novel method that finds the discrete optimal solution of such problems by maximizing the corresponding Lagrangian dual. This method can be applied to any constrained energy minimization problem whose unconstrained version is polynomial time solvable, and can handle multiple, equality or inequality, and linear or non-linear constraints. We demonstrate the efficacy of our method on the foreground/background image segmentation problem, and show that it produces impressive segmentation results with less error, and runs more than 20 times faster than the state-of-the-art LP relaxation based approaches.

Multi-dimensional Parametric Mincuts for Constrained MAP Inference

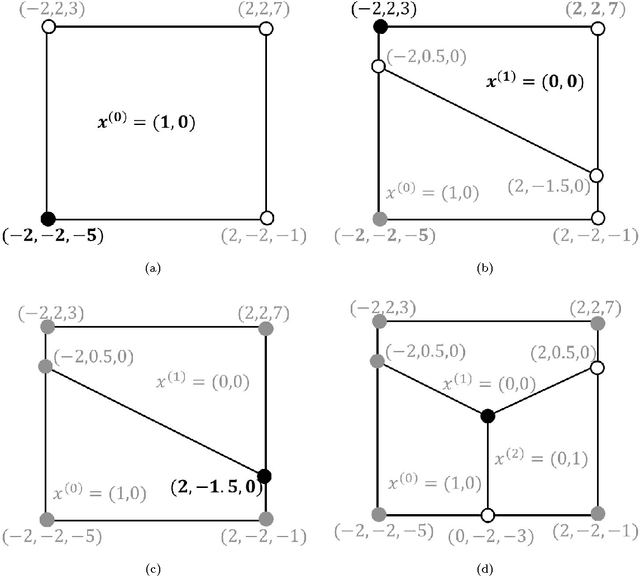
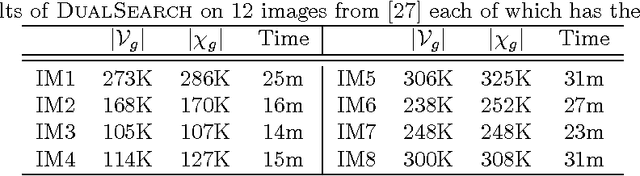
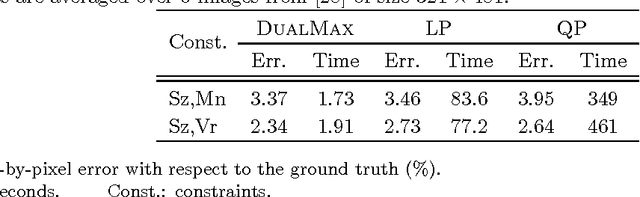
In this paper, we propose novel algorithms for inferring the Maximum a Posteriori (MAP) solution of discrete pairwise random field models under multiple constraints. We show how this constrained discrete optimization problem can be formulated as a multi-dimensional parametric mincut problem via its Lagrangian dual, and prove that our algorithm isolates all constraint instances for which the problem can be solved exactly. These multiple solutions enable us to even deal with `soft constraints' (higher order penalty functions). Moreover, we propose two practical variants of our algorithm to solve problems with hard constraints. We also show how our method can be applied to solve various constrained discrete optimization problems such as submodular minimization and shortest path computation. Experimental evaluation using the foreground-background image segmentation problem with statistic constraints reveals that our method is faster and its results are closer to the ground truth labellings compared with the popular continuous relaxation based methods.