Inverse analysis of granular flows using differentiable graph neural network simulator

Inverse problems in granular flows, such as landslides and debris flows, involve estimating material parameters or boundary conditions based on target runout profile. Traditional high-fidelity simulators for these inverse problems are computationally demanding, restricting the number of simulations possible. Additionally, their non-differentiable nature makes gradient-based optimization methods, known for their efficiency in high-dimensional problems, inapplicable. While machine learning-based surrogate models offer computational efficiency and differentiability, they often struggle to generalize beyond their training data due to their reliance on low-dimensional input-output mappings that fail to capture the complete physics of granular flows. We propose a novel differentiable graph neural network simulator (GNS) by combining reverse mode automatic differentiation of graph neural networks with gradient-based optimization for solving inverse problems. GNS learns the dynamics of granular flow by representing the system as a graph and predicts the evolution of the graph at the next time step, given the current state. The differentiable GNS shows optimization capabilities beyond the training data. We demonstrate the effectiveness of our method for inverse estimation across single and multi-parameter optimization problems, including evaluating material properties and boundary conditions for a target runout distance and designing baffle locations to limit a landslide runout. Our proposed differentiable GNS framework offers an orders of magnitude faster solution to these inverse problems than the conventional finite difference approach to gradient-based optimization.

Three-dimensional granular flow simulation using graph neural network-based learned simulator

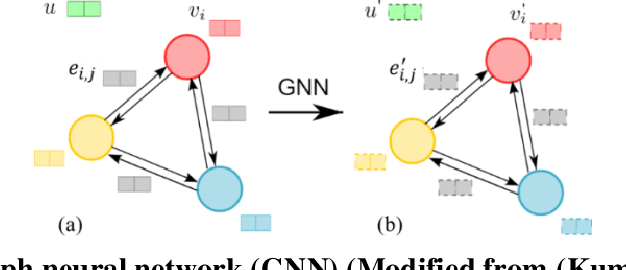
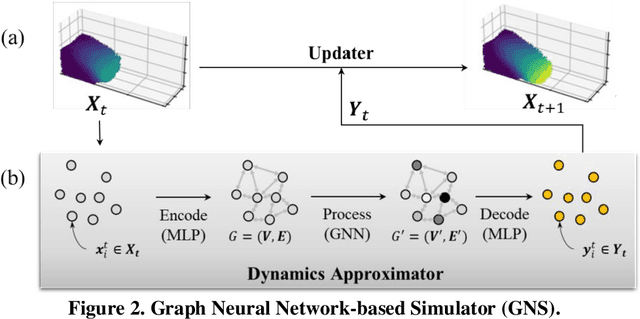
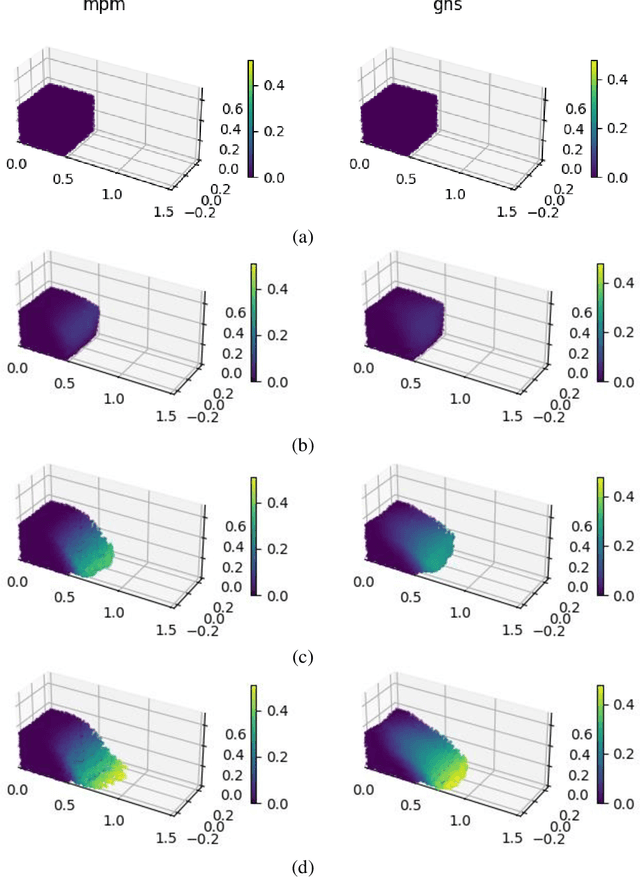
Reliable evaluations of geotechnical hazards like landslides and debris flow require accurate simulation of granular flow dynamics. Traditional numerical methods can simulate the complex behaviors of such flows that involve solid-like to fluid-like transitions, but they are computationally intractable when simulating large-scale systems. Surrogate models based on statistical or machine learning methods are a viable alternative, but they are typically empirical and rely on a confined set of parameters in evaluating associated risks. Due to their permutation-dependent learning, conventional machine learning models require an unreasonably large amount of training data for building generalizable surrogate models. We employ a graph neural network (GNN), a novel deep learning technique, to develop a GNN-based simulator (GNS) for granular flows to address these issues. Graphs represent the state of granular flows and interactions, like the exchange of energy and momentum between grains, and GNN learns the local interaction law. GNS takes the current state of the granular flow and estimates the next state using Euler explicit integration. We train GNS on a limited set of granular flow trajectories and evaluate its performance in a three-dimensional granular column collapse domain. GNS successfully reproduces the overall behaviors of column collapses with various aspect ratios that were not encountered during training. The computation speed of GNS outperforms high-fidelity numerical simulators by 300 times.

Accelerating Particle and Fluid Simulations with Differentiable Graph Networks for Solving Forward and Inverse Problems

We leverage physics-embedded differentiable graph network simulators (GNS) to accelerate particulate and fluid simulations to solve forward and inverse problems. GNS represents the domain as a graph with particles as nodes and learned interactions as edges. Compared to modeling global dynamics, GNS enables learning local interaction laws through edge messages, improving its generalization to new environments. GNS achieves over 165x speedup for granular flow prediction compared to parallel CPU numerical simulations. We propose a novel hybrid GNS/Material Point Method (MPM) to accelerate forward simulations by minimizing error on a pure surrogate model by interleaving MPM in GNS rollouts to satisfy conservation laws and minimize errors achieving 24x speedup compared to pure numerical simulations. The differentiable GNS enables solving inverse problems through automatic differentiation, identifying material parameters that result in target runout distances. We demonstrate the ability of GNS to solve inverse problems by iteratively updating the friction angle (a material property) by computing the gradient of a loss function based on the final and target runouts, thereby identifying the friction angle that best matches the observed runout. The physics-embedded and differentiable simulators open an exciting new paradigm for AI-accelerated design, control, and optimization.

Graph Neural Network-based surrogate model for granular flows

Accurate simulation of granular flow dynamics is crucial for assessing various geotechnical risks, including landslides and debris flows. Granular flows involve a dynamic rearrangement of particles exhibiting complex transitions from solid-like to fluid-like responses. Traditional continuum and discrete numerical methods are limited by their computational cost in simulating large-scale systems. Statistical or machine learning-based models offer an alternative. Still, they are largely empirical, based on a limited set of parameters. Due to their permutation-dependent learning, traditional machine learning-based models require huge training data to generalize. To resolve these problems, we use a graph neural network, a state-of-the-art machine learning architecture that learns local interactions. Graphs represent the state of dynamically changing granular flows and the interaction laws, such as energy and momentum exchange between grains. We develop a graph neural network-based simulator (GNS) that takes the current state of granular flow and predicts the next state using Euler explicit integration by learning the local interaction laws. We train GNS on different granular trajectories. We then assess the performance of GNS by predicting granular column collapse. GNS accurately predicts flow dynamics for column collapses with different aspect ratios unseen during training. GNS is hundreds of times faster than high-fidelity numerical simulators. The model also generalizes to domains much larger than the training data, handling more than twice the number of particles than it was trained on.

A machine learning approach to predicting pore pressure response in liquefiable sands under cyclic loading

Shear stress history controls the pore pressure response in liquefiable soils. The excess pore pressure does not increase under cyclic loading when shear stress amplitude is lower than the peak prior amplitude -- the shielding effect. Many sophisticated constitutive models fail to capture the shielding effect observed in the cyclic liquefaction experiments. We develop a data-driven machine learning model based on the LSTM neural network to capture the liquefaction response of soils under cyclic loading. The LSTM model is trained on 12 laboratory cyclic simple shear tests on Nevada sand in loose and dense conditions subjected to different cyclic simple shear loading conditions. The LSTM model features include the relative density of soil and the previous stress history to predict the pore water pressure response. The LSTM model successfully replicates the pore pressure response for three cyclic simple test results considering the shielding and density effects.

Semi-supervised Learning with Deep Generative Models for Asset Failure Prediction

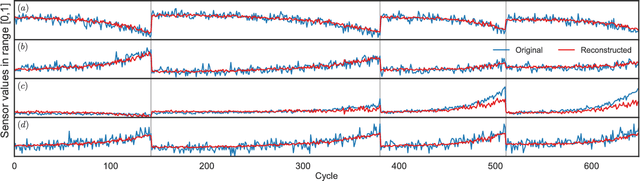
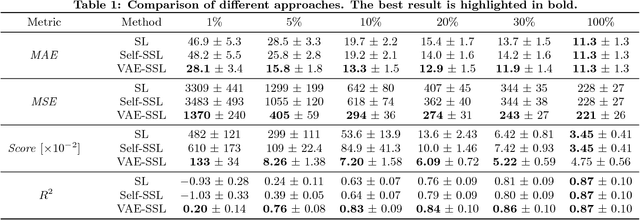
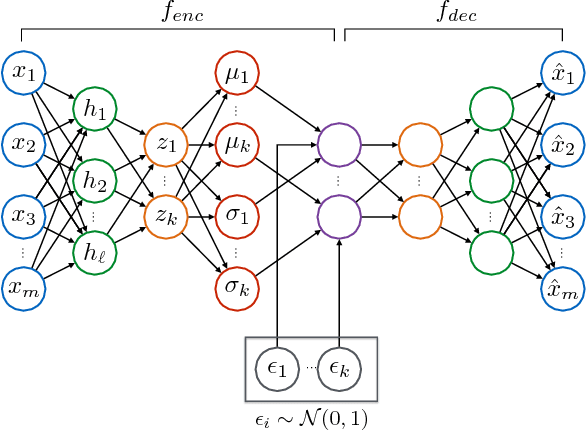
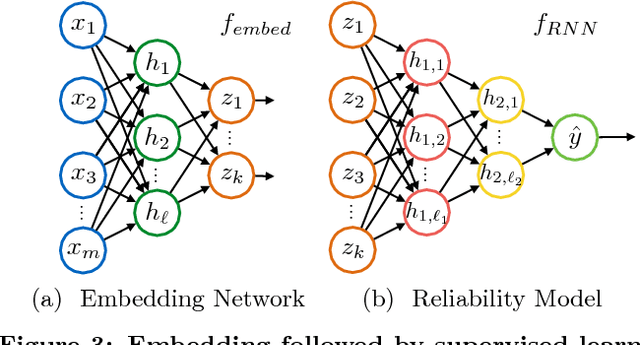
This work presents a novel semi-supervised learning approach for data-driven modeling of asset failures when health status is only partially known in historical data. We combine a generative model parameterized by deep neural networks with non-linear embedding technique. It allows us to build prognostic models with the limited amount of health status information for the precise prediction of future asset reliability. The proposed method is evaluated on a publicly available dataset for remaining useful life (RUL) estimation, which shows significant improvement even when a fraction of the data with known health status is as sparse as 1% of the total. Our study suggests that the non-linear embedding based on a deep generative model can efficiently regularize a complex model with deep architectures while achieving high prediction accuracy that is far less sensitive to the availability of health status information.