Vector Field-Guided Learning Predictive Control for Motion Planning of Mobile Robots with Unknown Dynamics

Safe maneuvering capability is critical for mobile robots in complex environments. However, robotic system dynamics are often time-varying, uncertain, or even unknown during the motion planning and control process. Therefore, many existing model-based reinforcement learning (RL) methods could not achieve satisfactory reliability in guaranteeing safety. To address this challenge, we propose a two-level Vector Field-guided Learning Predictive Control (VF-LPC) approach that guarantees safe maneuverability. The first level, the guiding level, generates safe desired trajectories using the designed kinodynamic guiding vector field, enabling safe motion in obstacle-dense environments. The second level, the Integrated Motion Planning and Control (IMPC) level, first uses the deep Koopman operator to learn a nominal dynamics model offline and then updates the model uncertainties online using sparse Gaussian processes (GPs). The learned dynamics and game-based safe barrier function are then incorporated into the learning predictive control framework to generate near-optimal control sequences. We conducted tests to compare the performance of VF-LPC with existing advanced planning methods in an obstacle-dense environment. The simulation results show that it can generate feasible trajectories quickly. Then, VF-LPC is evaluated against motion planning methods that employ model predictive control (MPC) and RL in high-fidelity CarSim software. The results show that VF-LPC outperforms them under metrics of completion time, route length, and average solution time. We also carried out path-tracking control tests on a racing road to validate the model uncertainties learning capability. Finally, we conducted real-world experiments on a Hongqi E-HS3 vehicle, further validating the VF-LPC approach's effectiveness.

CKNet: A Convolutional Neural Network Based on Koopman Operator for Modeling Latent Dynamics from Pixels

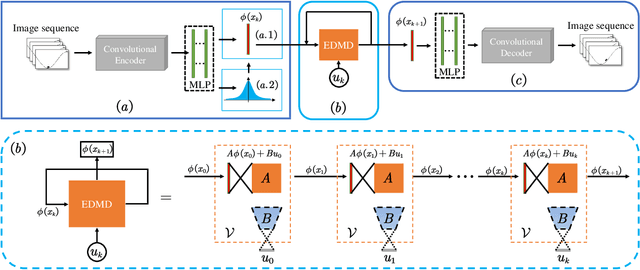
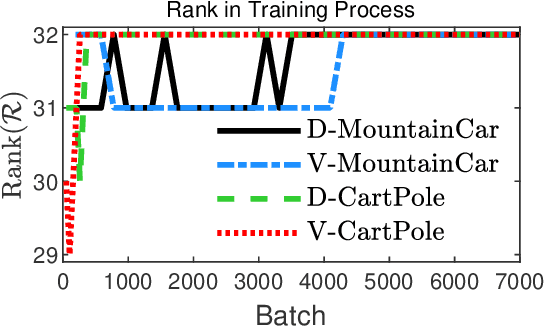
For systems with only known pixels, it is difficult to identify its dynamics, especially with a linear operator. In this work, we present a convolutional neural network (CNN) based on the Koopman operator (CKNet) to identify the latent dynamics from raw pixels. CKNet learned an encoder and decoder to play the role of the Koopman eigenfunctions and modes, respectively. The Koopman eigenvalues can be approximated by the eigenvalues of the learned system matrix. We present the deterministic and variational approaches to realize the encoder separately. Because CKNet is trained under the constraints of the Koopman theory, the identified dynamics is linear, controllable and physically-interpretable. Besides, the system matrix and control matrix are trained as trainable tensors. To improve the performance, we propose the auxiliary weight term for multi-step linearity and prediction losses. Experiments select two classic forced dynamical systems with continuous action space, and the results show that identified dynamics with 32-dim can predict validly 120 steps and generate clear images.