CKNet: A Convolutional Neural Network Based on Koopman Operator for Modeling Latent Dynamics from Pixels

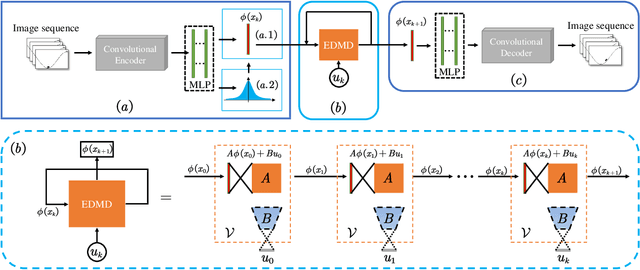
For systems with only known pixels, it is difficult to identify its dynamics, especially with a linear operator. In this work, we present a convolutional neural network (CNN) based on the Koopman operator (CKNet) to identify the latent dynamics from raw pixels. CKNet learned an encoder and decoder to play the role of the Koopman eigenfunctions and modes, respectively. The Koopman eigenvalues can be approximated by the eigenvalues of the learned system matrix. We present the deterministic and variational approaches to realize the encoder separately. Because CKNet is trained under the constraints of the Koopman theory, the identified dynamics is linear, controllable and physically-interpretable. Besides, the system matrix and control matrix are trained as trainable tensors. To improve the performance, we propose the auxiliary weight term for multi-step linearity and prediction losses. Experiments select two classic forced dynamical systems with continuous action space, and the results show that identified dynamics with 32-dim can predict validly 120 steps and generate clear images.