Numerical Uncertainty of Convolutional Neural Networks Inference for Structural Brain MRI Analysis

This paper investigates the numerical uncertainty of Convolutional Neural Networks (CNNs) inference for structural brain MRI analysis. It applies Random Rounding -- a stochastic arithmetic technique -- to CNN models employed in non-linear registration (SynthMorph) and whole-brain segmentation (FastSurfer), and compares the resulting numerical uncertainty to the one measured in a reference image-processing pipeline (FreeSurfer recon-all). Results obtained on 32 representative subjects show that CNN predictions are substantially more accurate numerically than traditional image-processing results (non-linear registration: 19 vs 13 significant bits on average; whole-brain segmentation: 0.99 vs 0.92 S{\o}rensen-Dice score on average), which suggests a better reproducibility of CNN results across execution environments.

Numerical Stability of DeepGOPlus Inference

Convolutional neural networks (CNNs) are currently among the most widely-used neural networks available and achieve state-of-the-art performance for many problems. While originally applied to computer vision tasks, CNNs work well with any data with a spatial relationship, besides images, and have been applied to different fields. However, recent works have highlighted how CNNs, like other deep learning models, are sensitive to noise injection which can jeopardise their performance. This paper quantifies the numerical uncertainty of the floating point arithmetic inaccuracies of the inference stage of DeepGOPlus, a CNN that predicts protein function, in order to determine its numerical stability. In addition, this paper investigates the possibility to use reduced-precision floating point formats for DeepGOPlus inference to reduce memory consumption and latency. This is achieved with Monte Carlo Arithmetic, a technique that experimentally quantifies floating point operation errors and VPREC, a tool that emulates results with customizable floating point precision formats. Focus is placed on the inference stage as it is the main deliverable of the DeepGOPlus model that will be used across environments and therefore most likely be subjected to the most amount of noise. Furthermore, studies have shown that the inference stage is the part of the model which is most disposed to being scaled down in terms of reduced precision. All in all, it has been found that the numerical uncertainty of the DeepGOPlus CNN is very low at its current numerical precision format, but the model cannot currently be reduced to a lower precision that might render it more lightweight.

Data Augmentation Through Monte Carlo Arithmetic Leads to More Generalizable Classification in Connectomics

Machine learning models are commonly applied to human brain imaging datasets in an effort to associate function or structure with behaviour, health, or other individual phenotypes. Such models often rely on low-dimensional maps generated by complex processing pipelines. However, the numerical instabilities inherent to pipelines limit the fidelity of these maps and introduce computational bias. Monte Carlo Arithmetic, a technique for introducing controlled amounts of numerical noise, was used to perturb a structural connectome estimation pipeline, ultimately producing a range of plausible networks for each sample. The variability in the perturbed networks was captured in an augmented dataset, which was then used for an age classification task. We found that resampling brain networks across a series of such numerically perturbed outcomes led to improved performance in all tested classifiers, preprocessing strategies, and dimensionality reduction techniques. Importantly, we find that this benefit does not hinge on a large number of perturbations, suggesting that even minimally perturbing a dataset adds meaningful variance which can be captured in the subsequently designed models.

Accurate simulation of operating system updates in neuroimaging using Monte-Carlo arithmetic

Operating system (OS) updates introduce numerical perturbations that impact the reproducibility of computational pipelines. In neuroimaging, this has important practical implications on the validity of computational results, particularly when obtained in systems such as high-performance computing clusters where the experimenter does not control software updates. We present a framework to reproduce the variability induced by OS updates in controlled conditions. We hypothesize that OS updates impact computational pipelines mainly through numerical perturbations originating in mathematical libraries, which we simulate using Monte-Carlo arithmetic in a framework called "fuzzy libmath" (FL). We applied this methodology to pre-processing pipelines of the Human Connectome Project, a flagship open-data project in neuroimaging. We found that FL-perturbed pipelines accurately reproduce the variability induced by OS updates and that this similarity is only mildly dependent on simulation parameters. Importantly, we also found between-subject differences were preserved in both cases, though the between-run variability was of comparable magnitude for both FL and OS perturbations. We found the numerical precision in the HCP pre-processed images to be relatively low, with less than 8 significant bits among the 24 available, which motivates further investigation of the numerical stability of components in the tested pipeline. Overall, our results establish that FL accurately simulates results variability due to OS updates, and is a practical framework to quantify numerical uncertainty in neuroimaging.

Reducing numerical precision preserves classification accuracy in Mondrian Forests

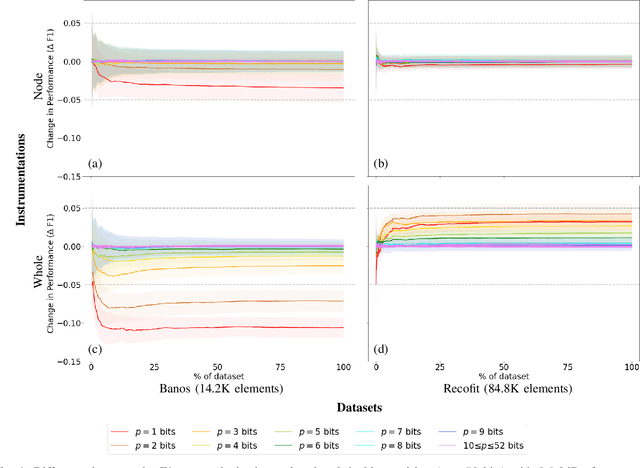
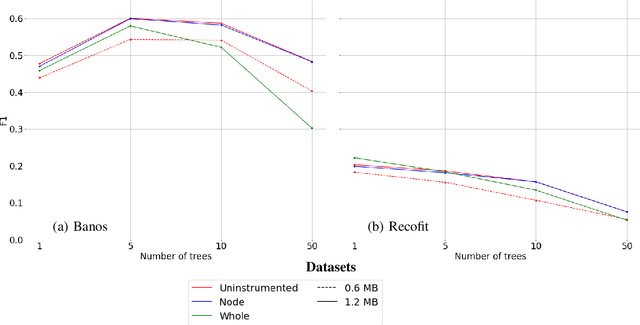
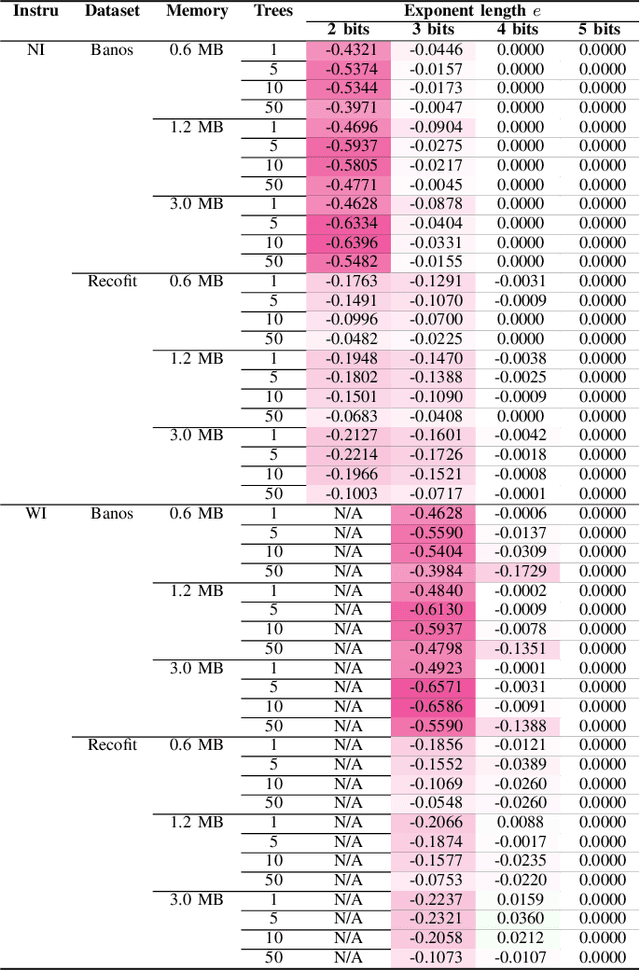
Mondrian Forests are a powerful data stream classification method, but their large memory footprint makes them ill-suited for low-resource platforms such as connected objects. We explored using reduced-precision floating-point representations to lower memory consumption and evaluated its effect on classification performance. We applied the Mondrian Forest implementation provided by OrpailleCC, a C++ collection of data stream algorithms, to two canonical datasets in human activity recognition: Recofit and Banos \emph{et al}. Results show that the precision of floating-point values used by tree nodes can be reduced from 64 bits to 8 bits with no significant difference in F1 score. In some cases, reduced precision was shown to improve classification performance, presumably due to its regularization effect. We conclude that numerical precision is a relevant hyperparameter in the Mondrian Forest, and that commonly-used double precision values may not be necessary for optimal performance. Future work will evaluate the generalizability of these findings to other data stream classifiers.