SAGE: Multi-Agent Self-Evolution for LLM Reasoning

Reinforcement learning with verifiable rewards improves reasoning in large language models (LLMs), but many methods still rely on large human-labeled datasets. While self-play reduces this dependency, it often lacks explicit planning and strong quality control, limiting stability in long-horizon multi-step reasoning. We present SAGE (Self-evolving Agents for Generalized reasoning Evolution), a closed-loop framework where four agents: Challenger, Planner, Solver, and Critic, co-evolve from a shared LLM backbone using only a small seed set. The Challenger continuously generates increasingly difficult tasks; the Planner converts each task into a structured multi-step plan; and the Solver follows the plan to produce an answer, whose correctness is determined by external verifiers. The Critic scores and filters both generated questions and plans to prevent curriculum drift and maintain training signal quality, enabling stable self-training. Across mathematics and code-generation benchmarks, SAGE delivers consistent gains across model scales, improving the Qwen-2.5-7B model by 8.9% on LiveCodeBench and 10.7% on OlympiadBench.

SEMAG: Self-Evolutionary Multi-Agent Code Generation

Large Language Models (LLMs) have made significant progress in handling complex programming tasks. However, current methods rely on manual model selection and fixed workflows, which limit their ability to adapt to changing task complexities. To address this, we propose SEMAG, a Self-Evolutionary Multi-Agent code Generation framework that mimics human coding practices. It decomposes programming tasks into stages, including planning, coding, debugging, and discussion, while adapting workflows to task difficulty. Its self-evolutionary agents can access the latest models in real time and automatically upgrade the backbone model. SEMAG sets new state-of-the-art Pass@1 accuracy across benchmarks. Using identical backbone models, SEMAG outperforms prior methods by 3.3% on CodeContests. When augmented with self-evolutionary model selection that automatically identifies optimal backbones, SEMAG reaches 52.6%, showcasing both framework effectiveness and adaptability to evolving LLM capabilities.

SceneRAG: Scene-level Retrieval-Augmented Generation for Video Understanding

Despite recent advances in retrieval-augmented generation (RAG) for video understanding, effectively understanding long-form video content remains underexplored due to the vast scale and high complexity of video data. Current RAG approaches typically segment videos into fixed-length chunks, which often disrupts the continuity of contextual information and fails to capture authentic scene boundaries. Inspired by the human ability to naturally organize continuous experiences into coherent scenes, we present SceneRAG, a unified framework that leverages large language models to segment videos into narrative-consistent scenes by processing ASR transcripts alongside temporal metadata. SceneRAG further sharpens these initial boundaries through lightweight heuristics and iterative correction. For each scene, the framework fuses information from both visual and textual modalities to extract entity relations and dynamically builds a knowledge graph, enabling robust multi-hop retrieval and generation that account for long-range dependencies. Experiments on the LongerVideos benchmark, featuring over 134 hours of diverse content, confirm that SceneRAG substantially outperforms prior baselines, achieving a win rate of up to 72.5 percent on generation tasks.

PAFT: Prompt-Agnostic Fine-Tuning

While Large Language Models (LLMs) adapt well to downstream tasks after fine-tuning, this adaptability often compromises prompt robustness, as even minor prompt variations can significantly degrade performance. To address this, we propose Prompt-Agnostic Fine-Tuning(PAFT), a simple yet effective approach that dynamically adjusts prompts during fine-tuning. This encourages the model to learn underlying task principles rather than overfitting to specific prompt formulations. PAFT operates in two stages: First, a diverse set of meaningful, synthetic candidate prompts is constructed. Second, during fine-tuning, prompts are randomly sampled from this set to create dynamic training inputs. Extensive experiments across diverse datasets and LLMs demonstrate that models trained with PAFT exhibit strong robustness and generalization across a wide range of prompts, including unseen ones. This enhanced robustness improves both model performance and inference speed while maintaining training efficiency. Ablation studies further confirm the effectiveness of PAFT.

Flexora: Flexible Low Rank Adaptation for Large Language Models

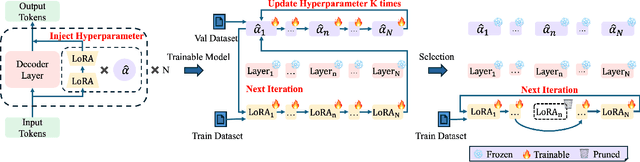
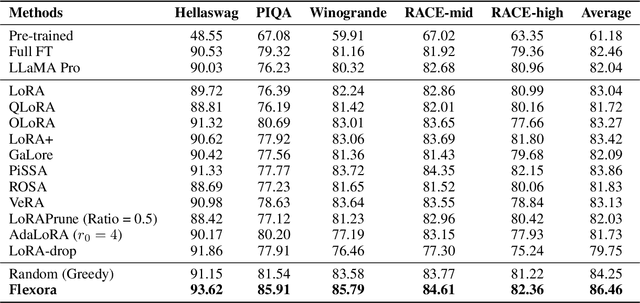
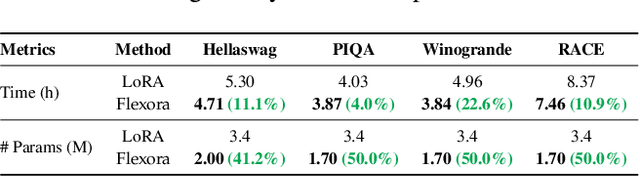
Large Language Models (LLMs) are driving advancements in artificial intelligence by increasing the scale of model parameters, which has significantly enhanced generalization ability and unlocked new capabilities in practice. However, their performance in specific downstream tasks is usually hindered by their knowledge boundaries on these tasks. Thus, fine-tuning techniques, especially the widely used Low-Rank Adaptation (LoRA) method, have been introduced to expand the boundaries on these tasks, whereas LoRA would underperform on certain tasks owing to its potential overfitting on these tasks. To overcome this overfitting and improve the performance of LoRA, we propose the flexible low rank adaptation (Flexora) method to automatically and flexibly select the most important layers needing to be fine-tuned to achieve the best performance on different downstream tasks. Specifically, Flexora firstly frames this layer selection problem as a well-defined hyperparameter optimization (HPO) problem, then addresses it using the unrolled differentiation (UD) method, and finally selects the most useful layers based on the optimized hyperparameters. Our extensive experiments on many pretrained models and natural language tasks show that Flexora is able to consistently improve over the existing baselines, indicating the effectiveness of our Flexora in practice. We additionally provide insightful theoretical results and many ablation studies to deliver a comprehensive understanding of our Flexora.

OptEx: Expediting First-Order Optimization with Approximately Parallelized Iterations

First-order optimization (FOO) algorithms are pivotal in numerous computational domains such as machine learning and signal denoising. However, their application to complex tasks like neural network training often entails significant inefficiencies due to the need for many sequential iterations for convergence. In response, we introduce first-order optimization expedited with approximately parallelized iterations (OptEx), the first framework that enhances the efficiency of FOO by leveraging parallel computing to mitigate its iterative bottleneck. OptEx employs kernelized gradient estimation to make use of gradient history for future gradient prediction, enabling parallelization of iterations -- a strategy once considered impractical because of the inherent iterative dependency in FOO. We provide theoretical guarantees for the reliability of our kernelized gradient estimation and the iteration complexity of SGD-based OptEx, confirming that estimation errors diminish to zero as historical gradients accumulate and that SGD-based OptEx enjoys an effective acceleration rate of $\Omega(\sqrt{N})$ over standard SGD given parallelism of N. We also use extensive empirical studies, including synthetic functions, reinforcement learning tasks, and neural network training across various datasets, to underscore the substantial efficiency improvements achieved by OptEx.