Weighted SGD for $\ell_p$ Regression with Randomized Preconditioning

In recent years, stochastic gradient descent (SGD) methods and randomized linear algebra (RLA) algorithms have been applied to many large-scale problems in machine learning and data analysis. We aim to bridge the gap between these two methods in solving constrained overdetermined linear regression problems---e.g., $\ell_2$ and $\ell_1$ regression problems. We propose a hybrid algorithm named pwSGD that uses RLA techniques for preconditioning and constructing an importance sampling distribution, and then performs an SGD-like iterative process with weighted sampling on the preconditioned system. We prove that pwSGD inherits faster convergence rates that only depend on the lower dimension of the linear system, while maintaining low computation complexity. Particularly, when solving $\ell_1$ regression with size $n$ by $d$, pwSGD returns an approximate solution with $\epsilon$ relative error in the objective value in $\mathcal{O}(\log n \cdot \text{nnz}(A) + \text{poly}(d)/\epsilon^2)$ time. This complexity is uniformly better than that of RLA methods in terms of both $\epsilon$ and $d$ when the problem is unconstrained. For $\ell_2$ regression, pwSGD returns an approximate solution with $\epsilon$ relative error in the objective value and the solution vector measured in prediction norm in $\mathcal{O}(\log n \cdot \text{nnz}(A) + \text{poly}(d) \log(1/\epsilon) /\epsilon)$ time. We also provide lower bounds on the coreset complexity for more general regression problems, indicating that still new ideas will be needed to extend similar RLA preconditioning ideas to weighted SGD algorithms for more general regression problems. Finally, the effectiveness of such algorithms is illustrated numerically on both synthetic and real datasets.

Trading Safety Versus Performance: Rapid Deployment of Robotic Swarms with Robust Performance Constraints

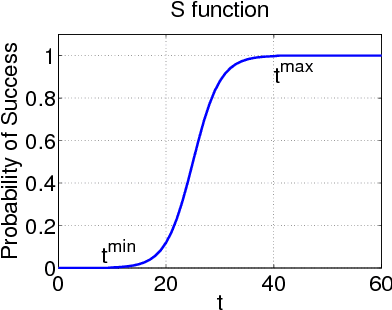
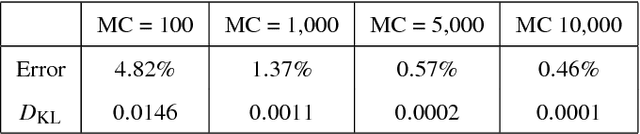
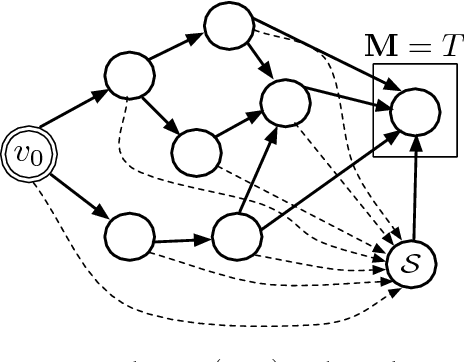
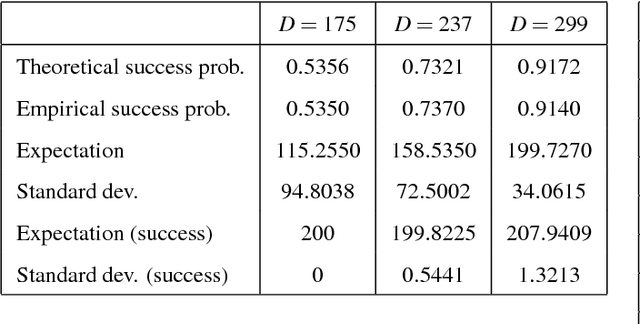
In this paper we consider a stochastic deployment problem, where a robotic swarm is tasked with the objective of positioning at least one robot at each of a set of pre-assigned targets while meeting a temporal deadline. Travel times and failure rates are stochastic but related, inasmuch as failure rates increase with speed. To maximize chances of success while meeting the deadline, a control strategy has therefore to balance safety and performance. Our approach is to cast the problem within the theory of constrained Markov Decision Processes, whereby we seek to compute policies that maximize the probability of successful deployment while ensuring that the expected duration of the task is bounded by a given deadline. To account for uncertainties in the problem parameters, we consider a robust formulation and we propose efficient solution algorithms, which are of independent interest. Numerical experiments confirming our theoretical results are presented and discussed.