Trading Safety Versus Performance: Rapid Deployment of Robotic Swarms with Robust Performance Constraints
Paper and Code
Nov 22, 2015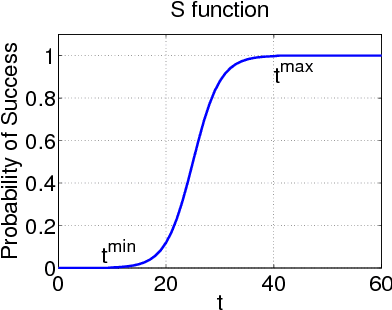
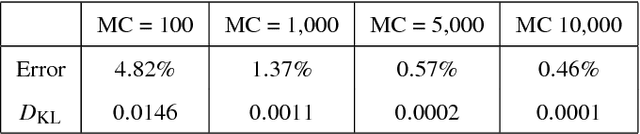
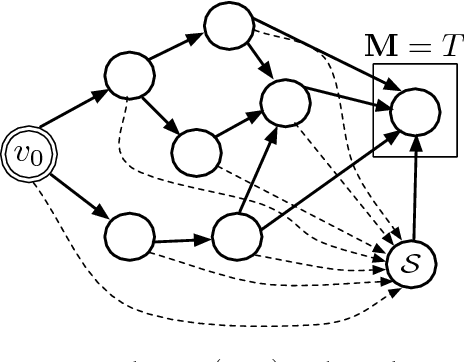
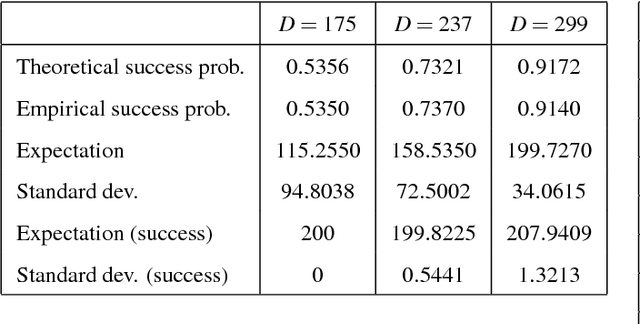
In this paper we consider a stochastic deployment problem, where a robotic swarm is tasked with the objective of positioning at least one robot at each of a set of pre-assigned targets while meeting a temporal deadline. Travel times and failure rates are stochastic but related, inasmuch as failure rates increase with speed. To maximize chances of success while meeting the deadline, a control strategy has therefore to balance safety and performance. Our approach is to cast the problem within the theory of constrained Markov Decision Processes, whereby we seek to compute policies that maximize the probability of successful deployment while ensuring that the expected duration of the task is bounded by a given deadline. To account for uncertainties in the problem parameters, we consider a robust formulation and we propose efficient solution algorithms, which are of independent interest. Numerical experiments confirming our theoretical results are presented and discussed.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge