Low-Complexity MUSIC Algorithm: From Finite-Precision Perspective

The high computational complexity of the multiple signal classification (MUSIC) algorithm is mainly caused by the subspace decomposition and spectrum search, especially for frequent real-time applications or massive sensors. In this paper, we propose a low-complexity MUSIC algorithm from finite-precision arithmetic perspective. First, we analyze the computational bottlenecks of the classic low-complexity randomized unitary-based MUSIC (RU-MUSIC), formulating this computational issue as an inner product problem. Then, a mixed-precision method is introduced to address this problem. Specifically, this method partitions summations in inner products into blocks, where intra-block computations use low-precision arithmetic and inter-block sums use high-precision arithmetic. To further improve computational accuracy, we develop an adaptive-precision method that supports adaptive block sizes and multiple precision levels. Finally, simulation results show that the proposed finite-precision MUSIC design achieves direction-of-arrival (DOA) estimation performance similar to that using full-precision arithmetic while reducing more than 50\% computational cost.

Mixed-Precision Quantization: Make the Best Use of Bits Where They Matter Most

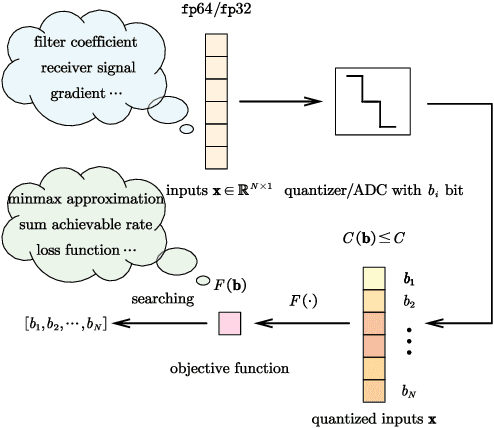
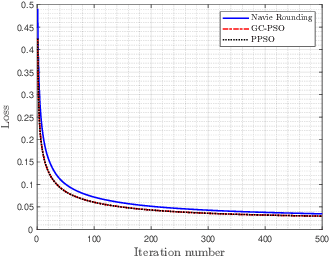
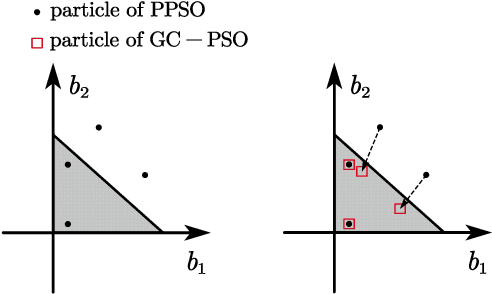
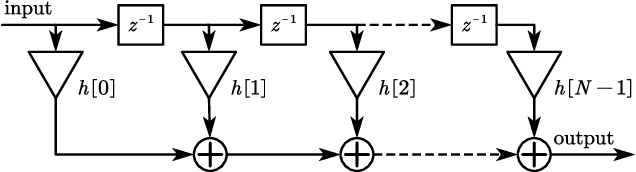
Mixed-precision quantization offers superior performance to fixed-precision quantization. It has been widely used in signal processing, communication systems, and machine learning. In mixed-precision quantization, bit allocation is essential. Hence, in this paper, we propose a new bit allocation framework for mixed-precision quantization from a search perspective. First, we formulate a general bit allocation problem for mixed-precision quantization. Then we introduce the penalized particle swarm optimization (PPSO) algorithm to address the integer consumption constraint. To improve efficiency and avoid iterations on infeasible solutions within the PPSO algorithm, a greedy criterion particle swarm optimization (GC-PSO) algorithm is proposed. The corresponding convergence analysis is derived based on dynamical system theory. Furthermore, we apply the above framework to some specific classic fields, i.e., finite impulse response (FIR) filters, receivers, and gradient descent. Numerical examples in each application underscore the superiority of the proposed framework to the existing algorithms.

FlowBotHD: History-Aware Diffuser Handling Ambiguities in Articulated Objects Manipulation

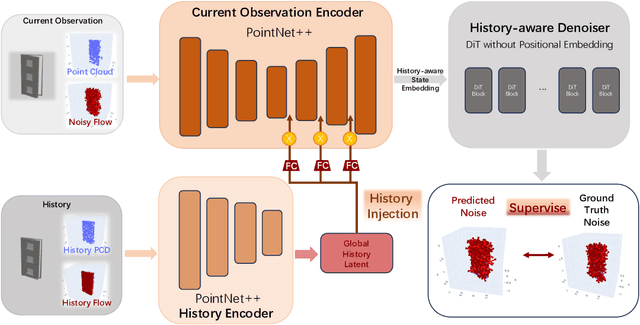
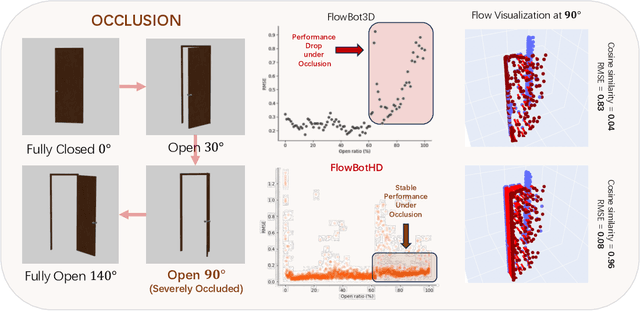
We introduce a novel approach to manipulate articulated objects with ambiguities, such as opening a door, in which multi-modality and occlusions create ambiguities about the opening side and direction. Multi-modality occurs when the method to open a fully closed door (push, pull, slide) is uncertain, or the side from which it should be opened is uncertain. Occlusions further obscure the door's shape from certain angles, creating further ambiguities during the occlusion. To tackle these challenges, we propose a history-aware diffusion network that models the multi-modal distribution of the articulated object and uses history to disambiguate actions and make stable predictions under occlusions. Experiments and analysis demonstrate the state-of-art performance of our method and specifically improvements in ambiguity-caused failure modes. Our project website is available at https://flowbothd.github.io/.

Finite-Precision Arithmetic Transceiver for Massive MIMO Systems

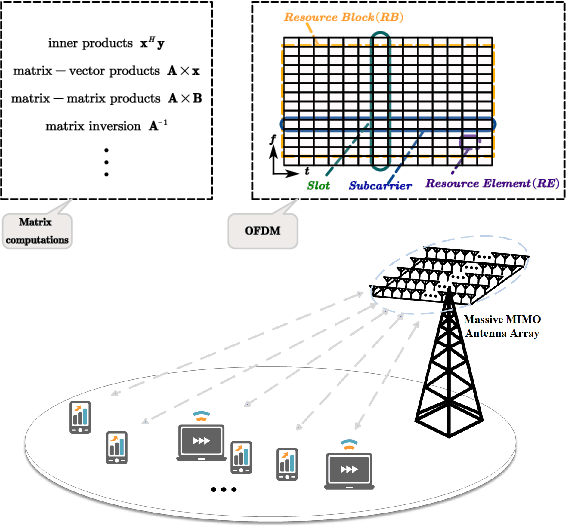
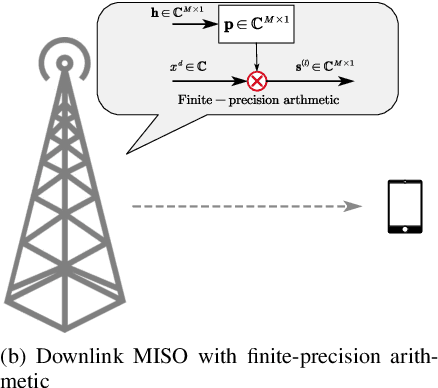
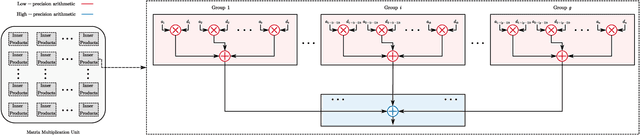
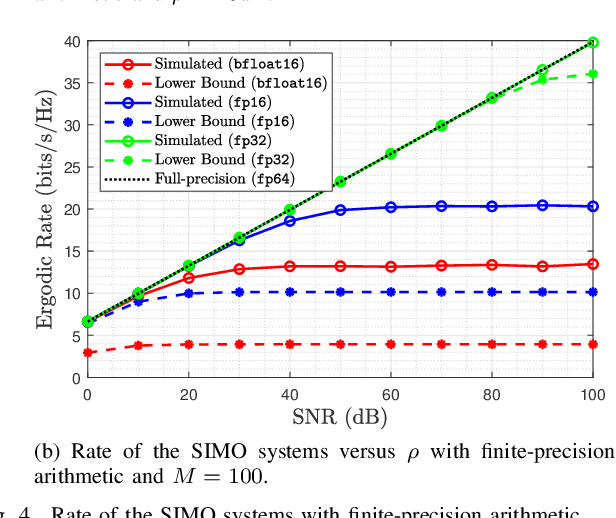
Efficient implementation of massive multiple-input-multiple-output (MIMO) transceivers is essential for the next-generation wireless networks. To reduce the high computational complexity of the massive MIMO transceiver, in this paper, we propose a new massive MIMO architecture using finite-precision arithmetic. First, we conduct the rounding error analysis and derive the lower bound of the achievable rate for single-input-multiple-output (SIMO) using maximal ratio combining (MRC) and multiple-input-single-output (MISO) systems using maximal ratio transmission (MRT) with finite-precision arithmetic. Then, considering the multi-user scenario, the rounding error analysis of zero-forcing (ZF) detection and precoding is derived by using the normal equations (NE) method. The corresponding lower bounds of the achievable sum rate are also derived and asymptotic analyses are presented. Built upon insights from these analyses and lower bounds, we propose a mixed-precision architecture for massive MIMO systems to offset performance gaps due to finite-precision arithmetic. The corresponding analysis of rounding errors and computational costs is obtained. Simulation results validate the derived bounds and underscore the superiority of the proposed mixed-precision architecture to the conventional structure.