Finite-Precision Arithmetic Transceiver for Massive MIMO Systems
Paper and Code
Feb 03, 2024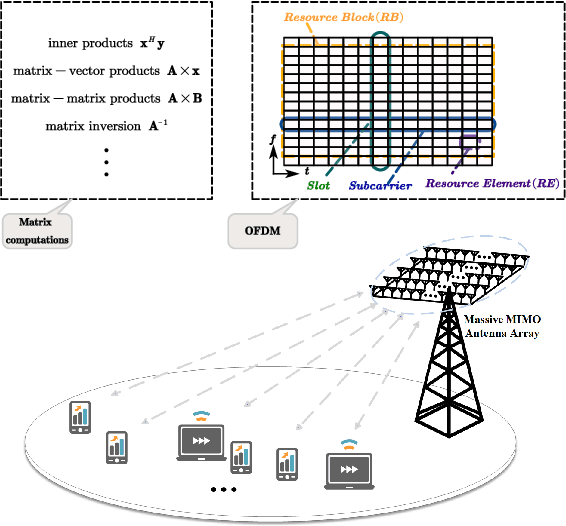
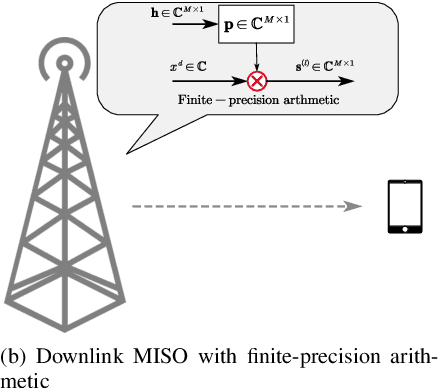
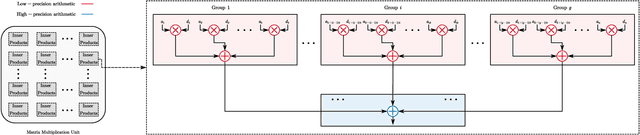
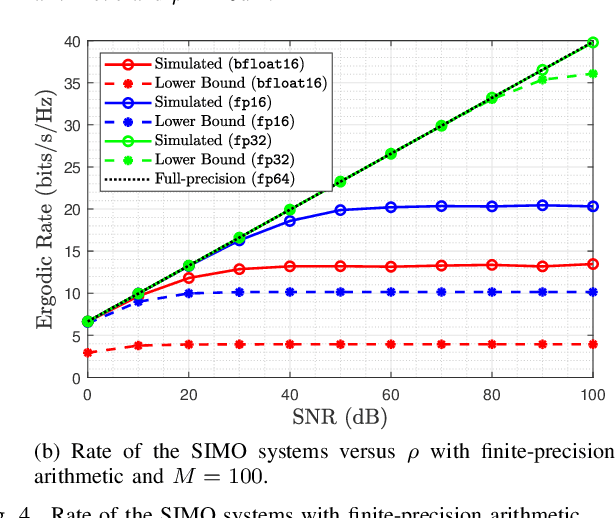
Efficient implementation of massive multiple-input-multiple-output (MIMO) transceivers is essential for the next-generation wireless networks. To reduce the high computational complexity of the massive MIMO transceiver, in this paper, we propose a new massive MIMO architecture using finite-precision arithmetic. First, we conduct the rounding error analysis and derive the lower bound of the achievable rate for single-input-multiple-output (SIMO) using maximal ratio combining (MRC) and multiple-input-single-output (MISO) systems using maximal ratio transmission (MRT) with finite-precision arithmetic. Then, considering the multi-user scenario, the rounding error analysis of zero-forcing (ZF) detection and precoding is derived by using the normal equations (NE) method. The corresponding lower bounds of the achievable sum rate are also derived and asymptotic analyses are presented. Built upon insights from these analyses and lower bounds, we propose a mixed-precision architecture for massive MIMO systems to offset performance gaps due to finite-precision arithmetic. The corresponding analysis of rounding errors and computational costs is obtained. Simulation results validate the derived bounds and underscore the superiority of the proposed mixed-precision architecture to the conventional structure.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge