Sharper Utility Bounds for Differentially Private Models

In this paper, by introducing Generalized Bernstein condition, we propose the first $\mathcal{O}\big(\frac{\sqrt{p}}{n\epsilon}\big)$ high probability excess population risk bound for differentially private algorithms under the assumptions $G$-Lipschitz, $L$-smooth, and Polyak-{\L}ojasiewicz condition, based on gradient perturbation method. If we replace the properties $G$-Lipschitz and $L$-smooth by $\alpha$-H{\"o}lder smoothness (which can be used in non-smooth setting), the high probability bound comes to $\mathcal{O}\big(n^{-\frac{\alpha}{1+2\alpha}}\big)$ w.r.t $n$, which cannot achieve $\mathcal{O}\left(1/n\right)$ when $\alpha\in(0,1]$. To solve this problem, we propose a variant of gradient perturbation method, \textbf{max$\{1,g\}$-Normalized Gradient Perturbation} (m-NGP). We further show that by normalization, the high probability excess population risk bound under assumptions $\alpha$-H{\"o}lder smooth and Polyak-{\L}ojasiewicz condition can achieve $\mathcal{O}\big(\frac{\sqrt{p}}{n\epsilon}\big)$, which is the first $\mathcal{O}\left(1/n\right)$ high probability excess population risk bound w.r.t $n$ for differentially private algorithms under non-smooth conditions. Moreover, we evaluate the performance of the new proposed algorithm m-NGP, the experimental results show that m-NGP improves the performance of the differentially private model over real datasets. It demonstrates that m-NGP improves the utility bound and the accuracy of the DP model on real datasets simultaneously.

Stability and Generalization of Differentially Private Minimax Problems

In the field of machine learning, many problems can be formulated as the minimax problem, including reinforcement learning, generative adversarial networks, to just name a few. So the minimax problem has attracted a huge amount of attentions from researchers in recent decades. However, there is relatively little work on studying the privacy of the general minimax paradigm. In this paper, we focus on the privacy of the general minimax setting, combining differential privacy together with minimax optimization paradigm. Besides, via algorithmic stability theory, we theoretically analyze the high probability generalization performance of the differentially private minimax algorithm under the strongly-convex-strongly-concave condition. To the best of our knowledge, this is the first time to analyze the generalization performance of general minimax paradigm, taking differential privacy into account.

Towards Sharper Utility Bounds for Differentially Private Pairwise Learning

Pairwise learning focuses on learning tasks with pairwise loss functions, depends on pairs of training instances, and naturally fits for modeling relationships between pairs of samples. In this paper, we focus on the privacy of pairwise learning and propose a new differential privacy paradigm for pairwise learning, based on gradient perturbation. Except for the privacy guarantees, we also analyze the excess population risk and give corresponding bounds under both expectation and high probability conditions. We use the \textit{on-average stability} and the \textit{pairwise locally elastic stability} theories to analyze the expectation bound and the high probability bound, respectively. Moreover, our analyzed utility bounds do not require convex pairwise loss functions, which means that our method is general to both convex and non-convex conditions. Under these circumstances, the utility bounds are similar to (or better than) previous bounds under convexity or strongly convexity assumption, which are attractive results.

Differentially Private ERM Based on Data Perturbation

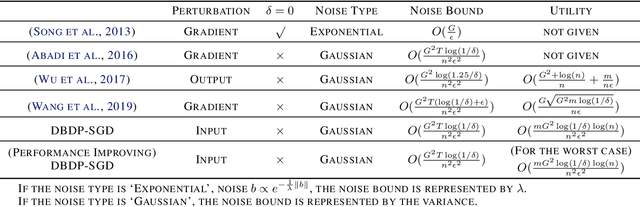
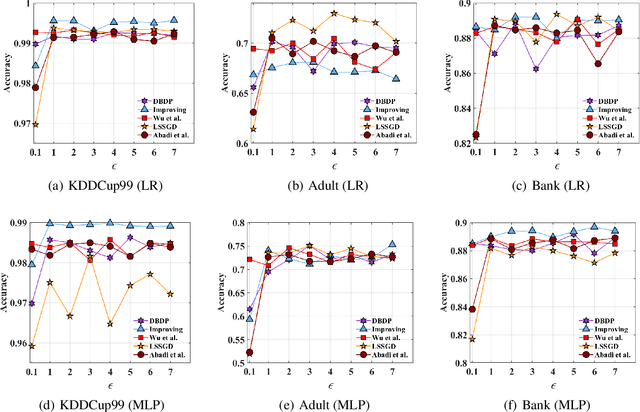
In this paper, after observing that different training data instances affect the machine learning model to different extents, we attempt to improve the performance of differentially private empirical risk minimization (DP-ERM) from a new perspective. Specifically, we measure the contributions of various training data instances on the final machine learning model, and select some of them to add random noise. Considering that the key of our method is to measure each data instance separately, we propose a new `Data perturbation' based (DB) paradigm for DP-ERM: adding random noise to the original training data and achieving ($\epsilon,\delta$)-differential privacy on the final machine learning model, along with the preservation on the original data. By introducing the Influence Function (IF), we quantitatively measure the impact of the training data on the final model. Theoretical and experimental results show that our proposed DBDP-ERM paradigm enhances the model performance significantly.

Input Perturbation: A New Paradigm between Central and Local Differential Privacy

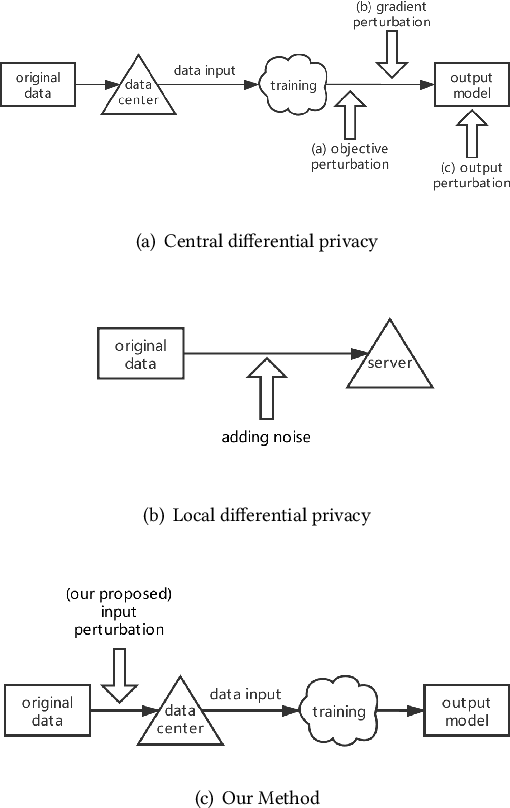
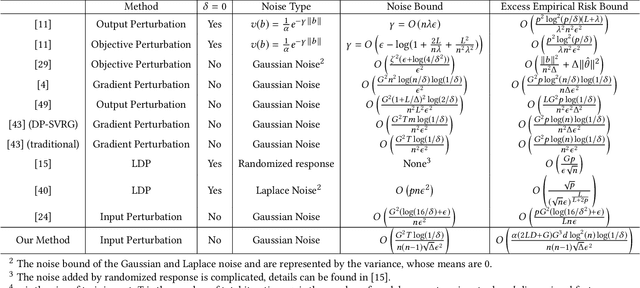
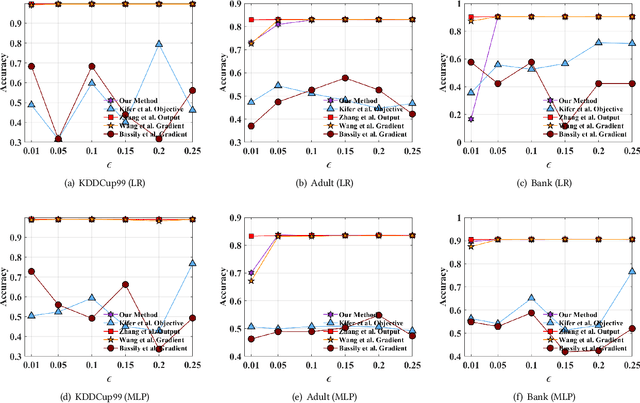
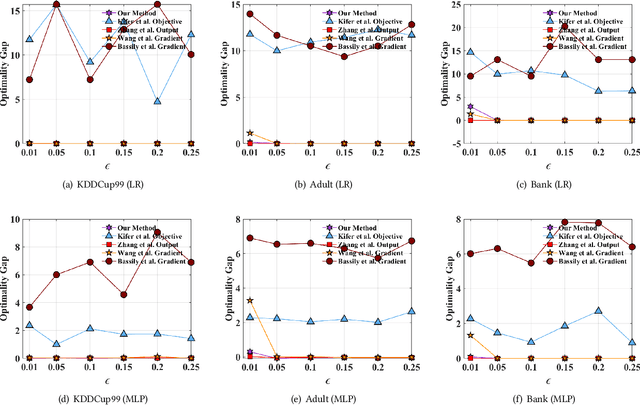
Traditionally, there are two models on differential privacy: the central model and the local model. The central model focuses on the machine learning model and the local model focuses on the training data. In this paper, we study the \textit{input perturbation} method in differentially private empirical risk minimization (DP-ERM), preserving privacy of the central model. By adding noise to the original training data and training with the `perturbed data', we achieve ($\epsilon$,$\delta$)-differential privacy on the final model, along with some kind of privacy on the original data. We observe that there is an interesting connection between the local model and the central model: the perturbation on the original data causes the perturbation on the gradient, and finally the model parameters. This observation means that our method builds a bridge between local and central model, protecting the data, the gradient and the model simultaneously, which is more superior than previous central methods. Detailed theoretical analysis and experiments show that our method achieves almost the same (or even better) performance as some of the best previous central methods with more protections on privacy, which is an attractive result. Moreover, we extend our method to a more general case: the loss function satisfies the Polyak-Lojasiewicz condition, which is more general than strong convexity, the constraint on the loss function in most previous work.

Weighted Distributed Differential Privacy ERM: Convex and Non-convex

Distributed machine learning is an approach allowing different parties to learn a model over all data sets without disclosing their own data. In this paper, we propose a weighted distributed differential privacy (WD-DP) empirical risk minimization (ERM) method to train a model in distributed setting, considering different weights of different clients. We guarantee differential privacy by gradient perturbation, adding Gaussian noise, and advance the state-of-the-art on gradient perturbation method in distributed setting. By detailed theoretical analysis, we show that in distributed setting, the noise bound and the excess empirical risk bound can be improved by considering different weights held by multiple parties. Moreover, considering that the constraint of convex loss function in ERM is not easy to achieve in some situations, we generalize our method to non-convex loss functions which satisfy Polyak-Lojasiewicz condition. Experiments on real data sets show that our method is more reliable and we improve the performance of distributed differential privacy ERM, especially in the case that data scale on different clients is uneven.