Input Perturbation: A New Paradigm between Central and Local Differential Privacy
Paper and Code
Feb 20, 2020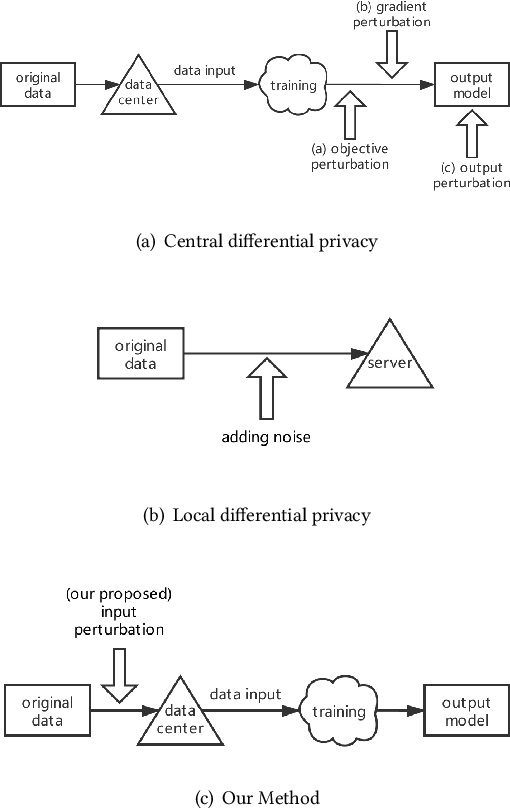
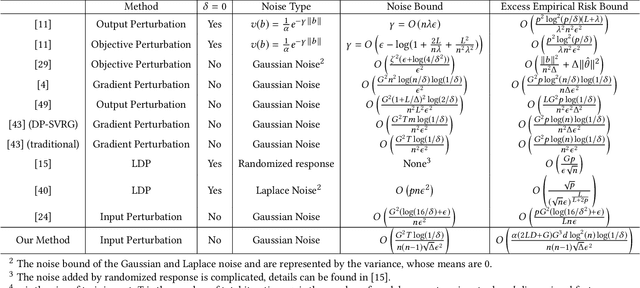
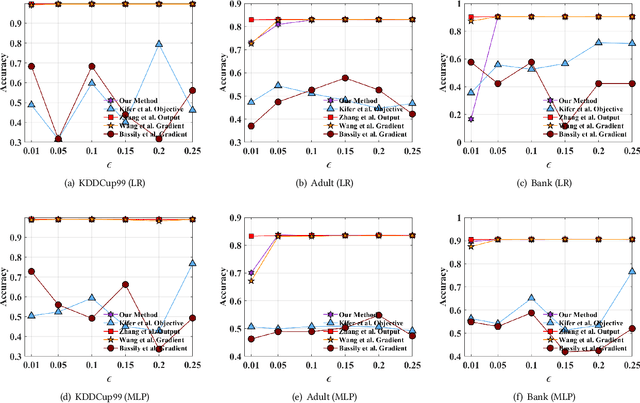
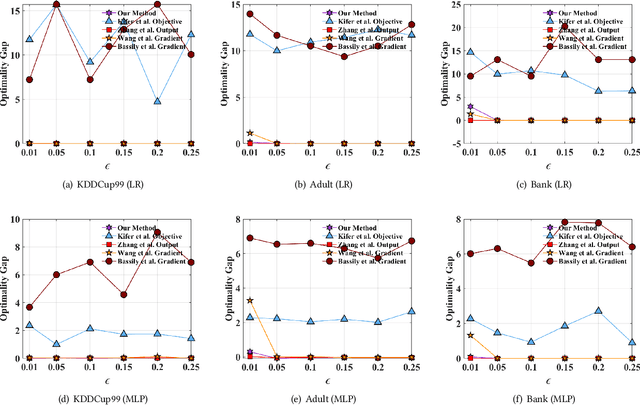
Traditionally, there are two models on differential privacy: the central model and the local model. The central model focuses on the machine learning model and the local model focuses on the training data. In this paper, we study the \textit{input perturbation} method in differentially private empirical risk minimization (DP-ERM), preserving privacy of the central model. By adding noise to the original training data and training with the `perturbed data', we achieve ($\epsilon$,$\delta$)-differential privacy on the final model, along with some kind of privacy on the original data. We observe that there is an interesting connection between the local model and the central model: the perturbation on the original data causes the perturbation on the gradient, and finally the model parameters. This observation means that our method builds a bridge between local and central model, protecting the data, the gradient and the model simultaneously, which is more superior than previous central methods. Detailed theoretical analysis and experiments show that our method achieves almost the same (or even better) performance as some of the best previous central methods with more protections on privacy, which is an attractive result. Moreover, we extend our method to a more general case: the loss function satisfies the Polyak-Lojasiewicz condition, which is more general than strong convexity, the constraint on the loss function in most previous work.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge