Reduction-based Pseudo-label Generation for Instance-dependent Partial Label Learning

Instance-dependent Partial Label Learning (ID-PLL) aims to learn a multi-class predictive model given training instances annotated with candidate labels related to features, among which correct labels are hidden fixed but unknown. The previous works involve leveraging the identification capability of the training model itself to iteratively refine supervision information. However, these methods overlook a critical aspect of ID-PLL: the training model is prone to overfitting on incorrect candidate labels, thereby providing poor supervision information and creating a bottleneck in training. In this paper, we propose to leverage reduction-based pseudo-labels to alleviate the influence of incorrect candidate labels and train our predictive model to overcome this bottleneck. Specifically, reduction-based pseudo-labels are generated by performing weighted aggregation on the outputs of a multi-branch auxiliary model, with each branch trained in a label subspace that excludes certain labels. This approach ensures that each branch explicitly avoids the disturbance of the excluded labels, allowing the pseudo-labels provided for instances troubled by these excluded labels to benefit from the unaffected branches. Theoretically, we demonstrate that reduction-based pseudo-labels exhibit greater consistency with the Bayes optimal classifier compared to pseudo-labels directly generated from the predictive model.

A spatio-temporal LSTM model to forecast across multiple temporal and spatial scales

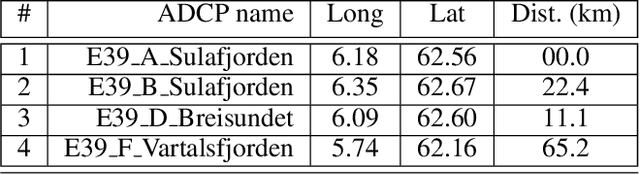
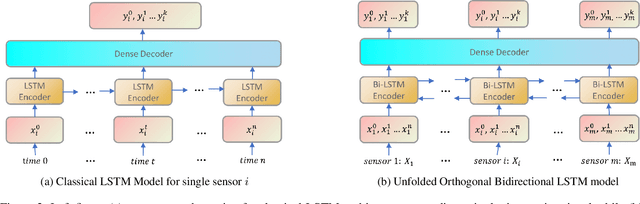
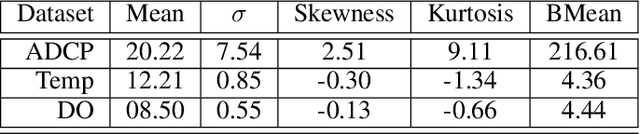
This paper presents a novel spatio-temporal LSTM (SPATIAL) architecture for time series forecasting applied to environmental datasets. The framework was evaluated across multiple sensors and for three different oceanic variables: current speed, temperature, and dissolved oxygen. Network implementation proceeded in two directions that are nominally separated but connected as part of a natural environmental system -- across the spatial (between individual sensors) and temporal components of the sensor data. Data from four sensors sampling current speed, and eight measuring both temperature and dissolved oxygen evaluated the framework. Results were compared against RF and XGB baseline models that learned on the temporal signal of each sensor independently by extracting the date-time features together with the past history of data using sliding window matrix. Results demonstrated ability to accurately replicate complex signals and provide comparable performance to state-of-the-art benchmarks. Notably, the novel framework provided a simpler pre-processing and training pipeline that handles missing values via a simple masking layer. Enabling learning across the spatial and temporal directions, this paper addresses two fundamental challenges of ML applications to environmental science: 1) data sparsity and the challenges and costs of collecting measurements of environmental conditions such as ocean dynamics, and 2) environmental datasets are inherently connected in the spatial and temporal directions while classical ML approaches only consider one of these directions. Furthermore, sharing of parameters across all input steps makes SPATIAL a fast, scalable, and easily-parameterized forecasting framework.

Neural Time-Dependent Partial Differential Equation

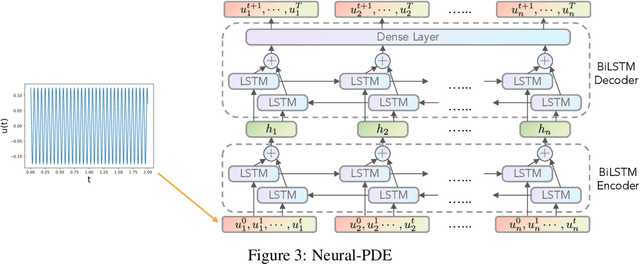
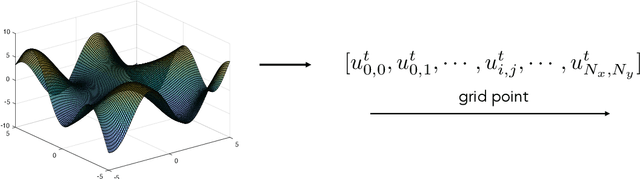
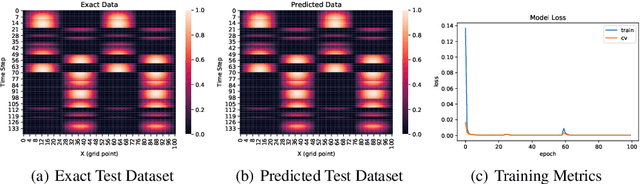
Partial differential equations (PDEs) play a crucial role in studying a vast number of problems in science and engineering. Numerically solving nonlinear and/or high-dimensional PDEs is often a challenging task. Inspired by the traditional finite difference and finite elements methods and emerging advancements in machine learning, we propose a sequence deep learning framework called Neural-PDE, which allows to automatically learn governing rules of any time-dependent PDE system from existing data by using a bidirectional LSTM encoder, and predict the next n time steps data. One critical feature of our proposed framework is that the Neural-PDE is able to simultaneously learn and simulate the multiscale variables.We test the Neural-PDE by a range of examples from one-dimensional PDEs to a high-dimensional and nonlinear complex fluids model. The results show that the Neural-PDE is capable of learning the initial conditions, boundary conditions and differential operators without the knowledge of the specific form of a PDE system.In our experiments the Neural-PDE can efficiently extract the dynamics within 20 epochs training, and produces accurate predictions. Furthermore, unlike the traditional machine learning approaches in learning PDE such as CNN and MLP which require vast parameters for model precision, Neural-PDE shares parameters across all time steps, thus considerably reduces the computational complexity and leads to a fast learning algorithm.