Structured Learning in Time-dependent Cox Models

Cox models with time-dependent coefficients and covariates are widely used in survival analysis. In high-dimensional settings, sparse regularization techniques are employed for variable selection, but existing methods for time-dependent Cox models lack flexibility in enforcing specific sparsity patterns (i.e., covariate structures). We propose a flexible framework for variable selection in time-dependent Cox models, accommodating complex selection rules. Our method can adapt to arbitrary grouping structures, including interaction selection, temporal, spatial, tree, and directed acyclic graph structures. It achieves accurate estimation with low false alarm rates. We develop the sox package, implementing a network flow algorithm for efficiently solving models with complex covariate structures. Sox offers a user-friendly interface for specifying grouping structures and delivers fast computation. Through examples, including a case study on identifying predictors of time to all-cause death in atrial fibrillation patients, we demonstrate the practical application of our method with specific selection rules.

Online Decisioning Meta-Heuristic Framework for Large Scale Black-Box Optimization

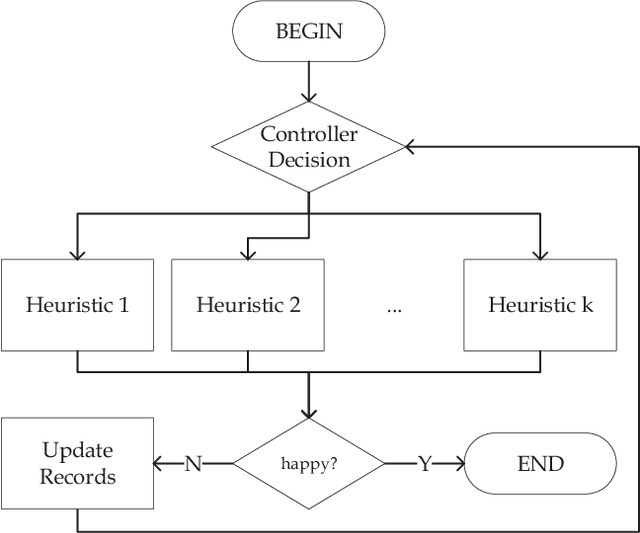
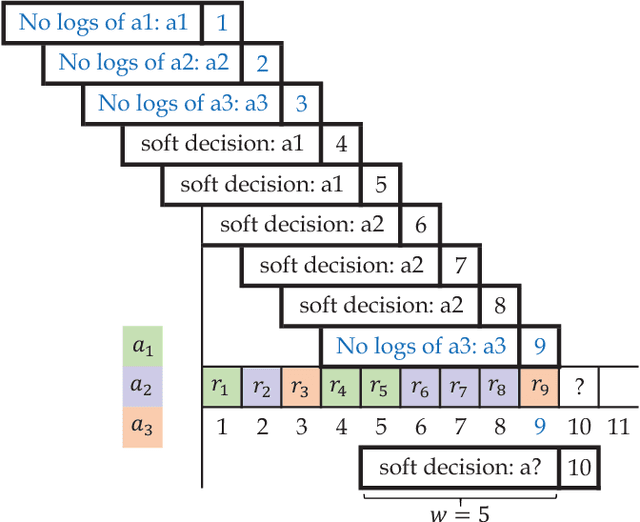
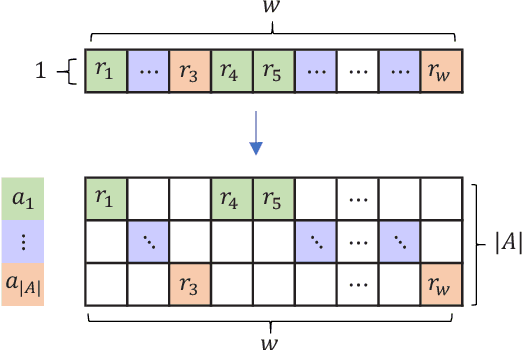
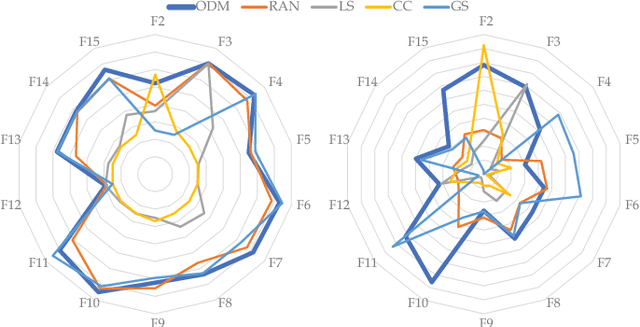
Out of practical concerns and with the expectation to achieve high overall efficiency of the resource utilization, this paper transforms the large scale black-box optimization problems with limited resources into online decision problems from the perspective of dynamic multi-armed bandits, a simplified view of Markov decision processes. The proposed Online Decisioning Meta-heuristic framework (ODM) is particularly well suited for real-world applications, with flexible compatibility for various kinds of costs, interfaces for easy heuristic articulation as well as fewer hyper-parameters for less variance in performance. Experimental results on benchmark functions suggest that ODM has demonstrated significant capabilities for online decisioning. Furthermore, when ODM is articulated with three heuristics, competitive performance can be achieved on benchmark problems with search dimensions up to 10000.