Yetong Zhang
Distributed Client-Server Optimization for SLAM with Limited On-Device Resources
Mar 26, 2021
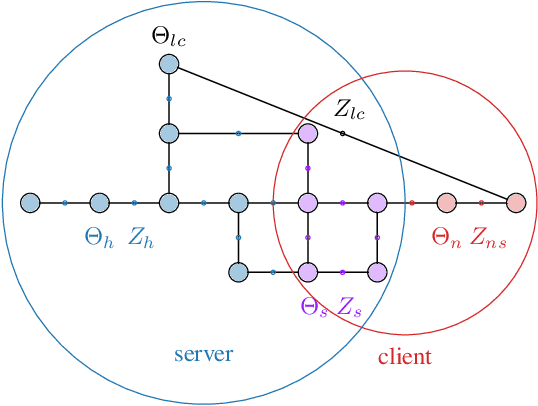
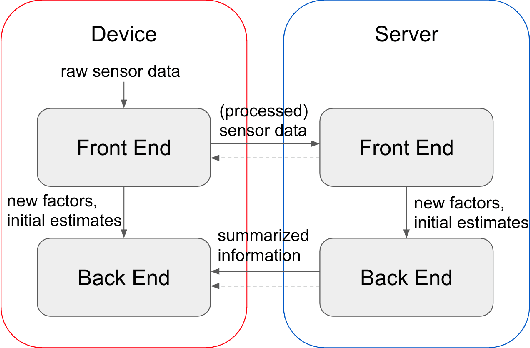
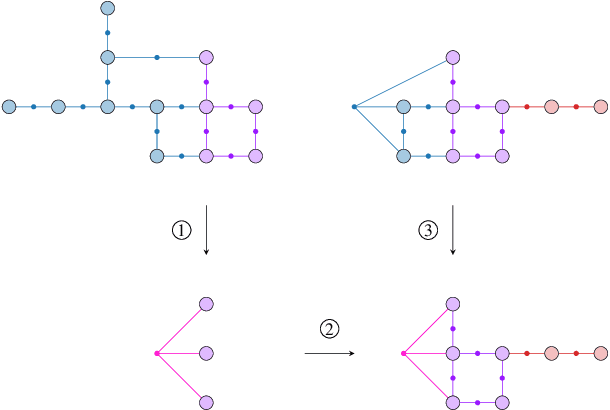
Abstract:Simultaneous localization and mapping (SLAM) is a crucial functionality for exploration robots and virtual/augmented reality (VR/AR) devices. However, some of such devices with limited resources cannot afford the computational or memory cost to run full SLAM algorithms. We propose a general client-server SLAM optimization framework that achieves accurate real-time state estimation on the device with low requirements of on-board resources. The resource-limited device (the client) only works on a small part of the map, and the rest of the map is processed by the server. By sending the summarized information of the rest of map to the client, the on-device state estimation is more accurate. Further improvement of accuracy is achieved in the presence of on-device early loop closures, which enables reloading useful variables from the server to the client. Experimental results from both synthetic and real-world datasets demonstrate that the proposed optimization framework achieves accurate estimation in real-time with limited computation and memory budget of the device.
Equality Constrained Linear Optimal Control With Factor Graphs
Nov 02, 2020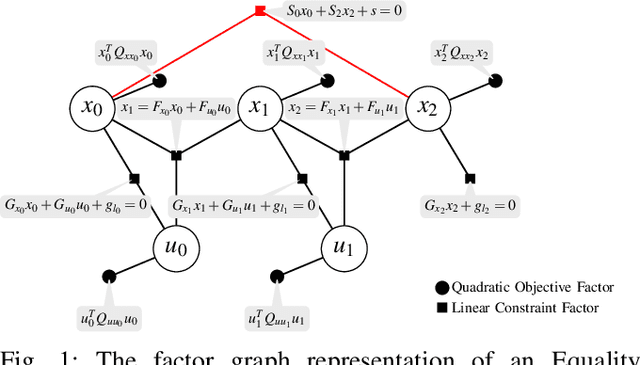
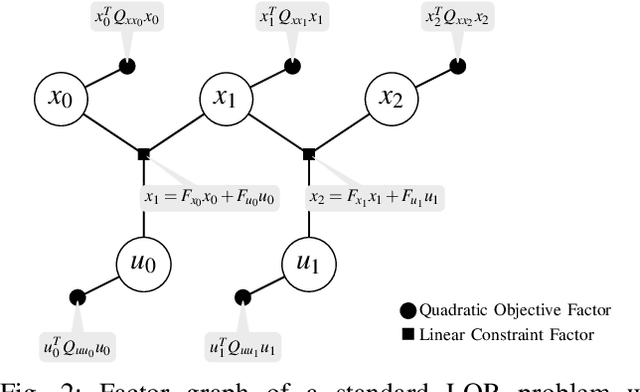
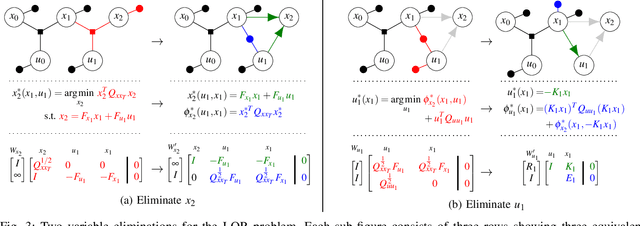
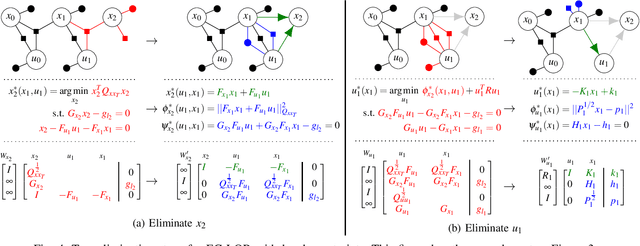
Abstract:This paper presents a novel factor graph-based approach to solve the discrete-time finite-horizon Linear Quadratic Regulator problem subject to auxiliary linear equality constraints within and across time steps. We represent such optimal control problems using constrained factor graphs and optimize the factor graphs to obtain the optimal trajectory and the feedback control policies using the variable elimination algorithm with a modified Gram-Schmidt process. We prove that our approach has the same order of computational complexity as the state-of-the-art dynamic programming approach. Furthermore, current dynamic programming approaches can only handle equality constraints between variables at the same time step, but ours can handle equality constraints among any combination of variables at any time step while maintaining linear complexity with respect to trajectory length. Our approach can be used to efficiently generate trajectories and feedback control policies to achieve periodic motion or repetitive manipulation.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge