Equality Constrained Linear Optimal Control With Factor Graphs
Paper and Code
Nov 02, 2020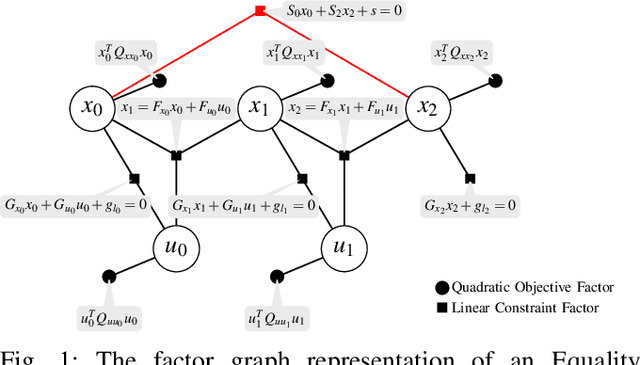
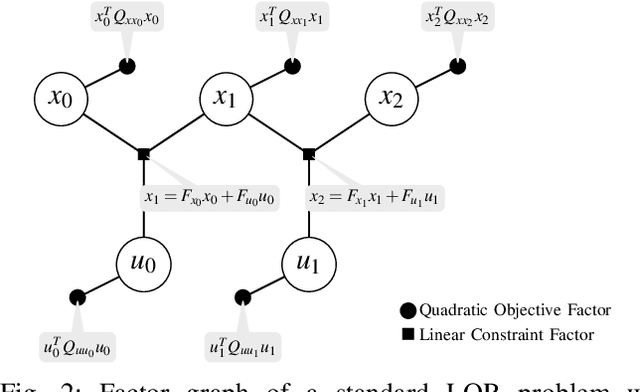
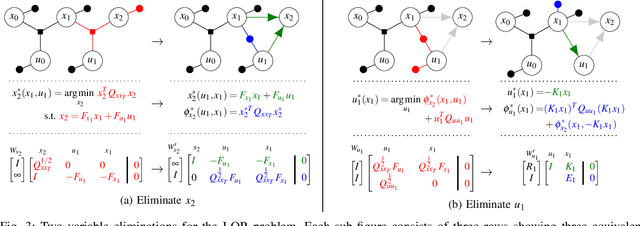
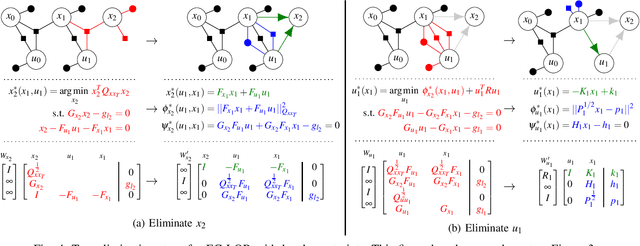
This paper presents a novel factor graph-based approach to solve the discrete-time finite-horizon Linear Quadratic Regulator problem subject to auxiliary linear equality constraints within and across time steps. We represent such optimal control problems using constrained factor graphs and optimize the factor graphs to obtain the optimal trajectory and the feedback control policies using the variable elimination algorithm with a modified Gram-Schmidt process. We prove that our approach has the same order of computational complexity as the state-of-the-art dynamic programming approach. Furthermore, current dynamic programming approaches can only handle equality constraints between variables at the same time step, but ours can handle equality constraints among any combination of variables at any time step while maintaining linear complexity with respect to trajectory length. Our approach can be used to efficiently generate trajectories and feedback control policies to achieve periodic motion or repetitive manipulation.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge