Artemis: HE-Aware Training for Efficient Privacy-Preserving Machine Learning

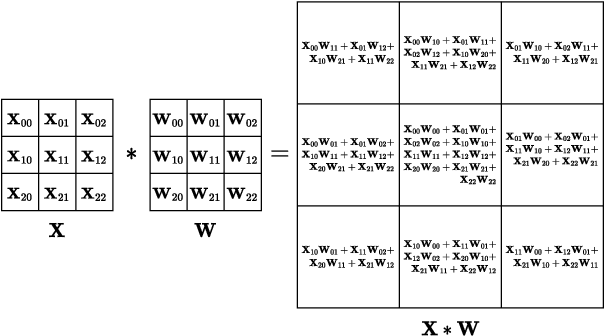
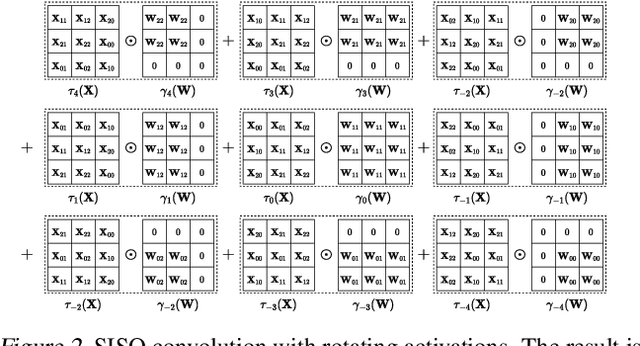
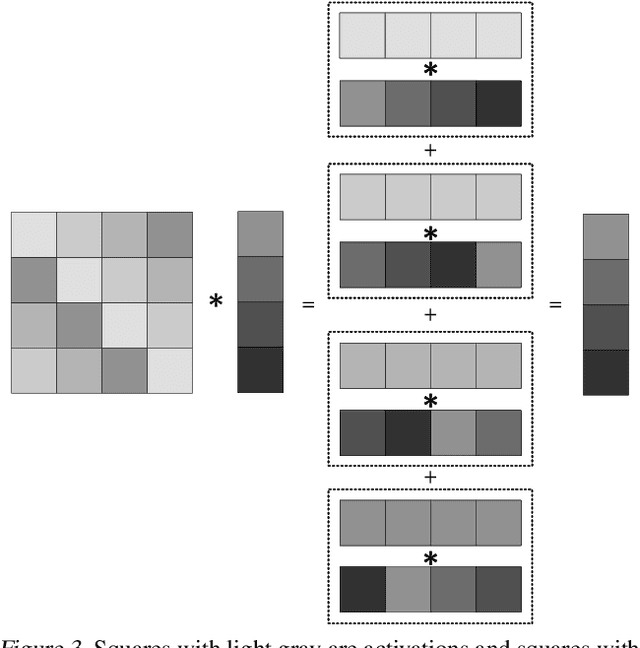
Privacy-Preserving ML (PPML) based on Homomorphic Encryption (HE) is a promising foundational privacy technology. Making it more practical requires lowering its computational cost, especially, in handling modern large deep neural networks. Model compression via pruning is highly effective in conventional plaintext ML but cannot be effectively applied to HE-PPML as is. We propose Artemis, a highly effective DNN pruning technique for HE-based inference. We judiciously investigate two HE-aware pruning strategies (positional and diagonal) to reduce the number of Rotation operations, which dominate compute time in HE convolution. We find that Pareto-optimal solutions are based fully on diagonal pruning. Artemis' benefits come from coupling DNN training, driven by a novel group Lasso regularization objective, with pruning to maximize HE-specific cost reduction (dominated by the Rotation operations). We show that Artemis improves on prior HE-oriented pruning and can achieve a 1.2-6x improvement when targeting modern convolutional models (ResNet18 and ResNet18) across three datasets.

A Provably Secure Strong PUF based on LWE: Construction and Implementation

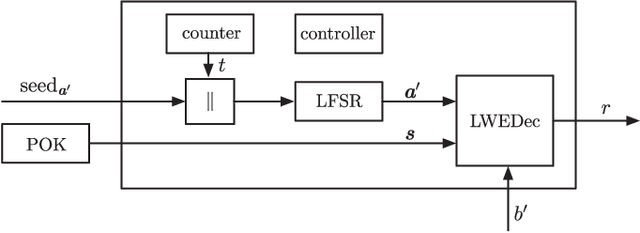
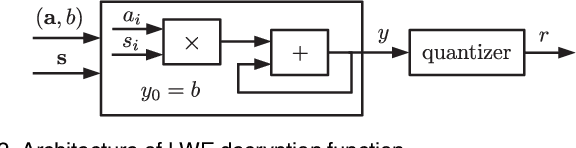
We construct a strong PUF with provable security against ML attacks on both classical and quantum computers. The security is guaranteed by the cryptographic hardness of learning decryption functions of public-key cryptosystems, and the hardness of the learning-with-errors (LWE) problem defined on integer lattices. We call our construction the lattice PUF. We construct lattice PUF with a physically obfuscated key and an LWE decryption function block. To allow deployments in different scenarios, we demonstrate designs with different latency-area trade-offs. A compact design uses a highly serialized LFSR and LWE decryption function, while a latency-optimized design uses an unrolled LFSR and a parallel datapath. We prototype lattice PUF designs with $2^{136}$ challenge-response pairs (CRPs) on a Spartan 6 FPGA. In addition to theoretical security guarantee, we evaluate empirical resistance to the various leading ML techniques: the prediction error remains above $49.76\%$ after $1$ million training CRPs. The resource-efficient design requires only $45$ slices for the PUF logic proper, and $351$ slices for a fuzzy extractor. The latency-optimized design achieves a $148X$ reduction in latency, at a $10X$ increase in PUF hardware utilization. The mean uniformity of PUF responses is $49.98\%$, the mean uniqueness is $50.00\%$, and the mean reliability is $1.26\%$.