A Provably Secure Strong PUF based on LWE: Construction and Implementation
Paper and Code
Mar 05, 2023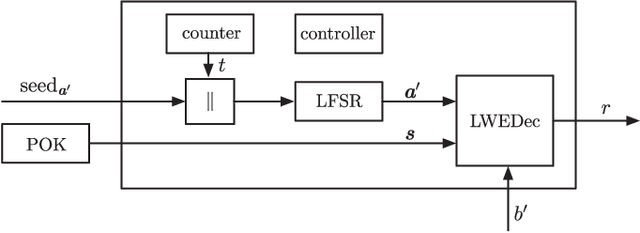

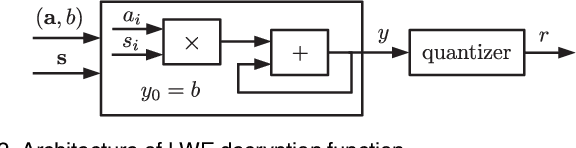

We construct a strong PUF with provable security against ML attacks on both classical and quantum computers. The security is guaranteed by the cryptographic hardness of learning decryption functions of public-key cryptosystems, and the hardness of the learning-with-errors (LWE) problem defined on integer lattices. We call our construction the lattice PUF. We construct lattice PUF with a physically obfuscated key and an LWE decryption function block. To allow deployments in different scenarios, we demonstrate designs with different latency-area trade-offs. A compact design uses a highly serialized LFSR and LWE decryption function, while a latency-optimized design uses an unrolled LFSR and a parallel datapath. We prototype lattice PUF designs with $2^{136}$ challenge-response pairs (CRPs) on a Spartan 6 FPGA. In addition to theoretical security guarantee, we evaluate empirical resistance to the various leading ML techniques: the prediction error remains above $49.76\%$ after $1$ million training CRPs. The resource-efficient design requires only $45$ slices for the PUF logic proper, and $351$ slices for a fuzzy extractor. The latency-optimized design achieves a $148X$ reduction in latency, at a $10X$ increase in PUF hardware utilization. The mean uniformity of PUF responses is $49.98\%$, the mean uniqueness is $50.00\%$, and the mean reliability is $1.26\%$.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge