Robust Reinforcement Learning under Diffusion Models for Data with Jumps

Reinforcement Learning (RL) has proven effective in solving complex decision-making tasks across various domains, but challenges remain in continuous-time settings, particularly when state dynamics are governed by stochastic differential equations (SDEs) with jump components. In this paper, we address this challenge by introducing the Mean-Square Bipower Variation Error (MSBVE) algorithm, which enhances robustness and convergence in scenarios involving significant stochastic noise and jumps. We first revisit the Mean-Square TD Error (MSTDE) algorithm, commonly used in continuous-time RL, and highlight its limitations in handling jumps in state dynamics. The proposed MSBVE algorithm minimizes the mean-square quadratic variation error, offering improved performance over MSTDE in environments characterized by SDEs with jumps. Simulations and formal proofs demonstrate that the MSBVE algorithm reliably estimates the value function in complex settings, surpassing MSTDE's performance when faced with jump processes. These findings underscore the importance of alternative error metrics to improve the resilience and effectiveness of RL algorithms in continuous-time frameworks.

SGD Distributional Dynamics of Three Layer Neural Networks

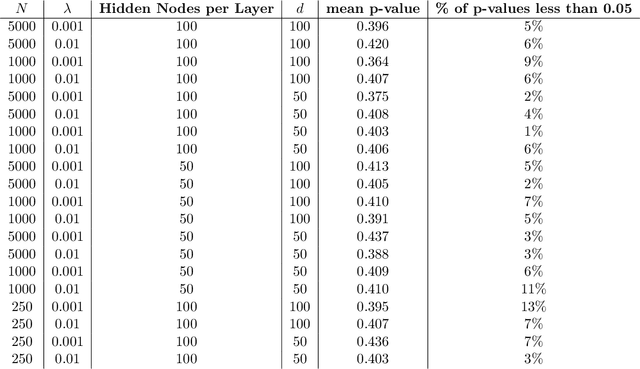
With the rise of big data analytics, multi-layer neural networks have surfaced as one of the most powerful machine learning methods. However, their theoretical mathematical properties are still not fully understood. Training a neural network requires optimizing a non-convex objective function, typically done using stochastic gradient descent (SGD). In this paper, we seek to extend the mean field results of Mei et al. (2018) from two-layer neural networks with one hidden layer to three-layer neural networks with two hidden layers. We will show that the SGD dynamics is captured by a set of non-linear partial differential equations, and prove that the distributions of weights in the two hidden layers are independent. We will also detail exploratory work done based on simulation and real-world data.

Optimal High-order Tensor SVD via Tensor-Train Orthogonal Iteration

This paper studies a general framework for high-order tensor SVD. We propose a new computationally efficient algorithm, tensor-train orthogonal iteration (TTOI), that aims to estimate the low tensor-train rank structure from the noisy high-order tensor observation. The proposed TTOI consists of initialization via TT-SVD (Oseledets, 2011) and new iterative backward/forward updates. We develop the general upper bound on estimation error for TTOI with the support of several new representation lemmas on tensor matricizations. By developing a matching information-theoretic lower bound, we also prove that TTOI achieves the minimax optimality under the spiked tensor model. The merits of the proposed TTOI are illustrated through applications to estimation and dimension reduction of high-order Markov processes, numerical studies, and a real data example on New York City taxi travel records. The software of the proposed algorithm is available online.

How Many Factors Influence Minima in SGD?

Stochastic gradient descent (SGD) is often applied to train Deep Neural Networks (DNNs), and research efforts have been devoted to investigate the convergent dynamics of SGD and minima found by SGD. The influencing factors identified in the literature include learning rate, batch size, Hessian, and gradient covariance, and stochastic differential equations are used to model SGD and establish the relationships among these factors for characterizing minima found by SGD. It has been found that the ratio of batch size to learning rate is a main factor in highlighting the underlying SGD dynamics; however, the influence of other important factors such as the Hessian and gradient covariance is not entirely agreed upon. This paper describes the factors and relationships in the recent literature and presents numerical findings on the relationships. In particular, it confirms the four-factor and general relationship results obtained in Wang (2019), while the three-factor and associated relationship results found in Jastrz\c{e}bski et al. (2018) may not hold beyond the considered special case.

Asymptotic Analysis via Stochastic Differential Equations of Gradient Descent Algorithms in Statistical and Computational Paradigms

This paper investigates asymptotic behaviors of gradient descent algorithms (particularly accelerated gradient descent and stochastic gradient descent) in the context of stochastic optimization arose in statistics and machine learning where objective functions are estimated from available data. We show that these algorithms can be modeled by continuous-time ordinary or stochastic differential equations, and their asymptotic dynamic evolutions and distributions are governed by some linear ordinary or stochastic differential equations, as the data size goes to infinity. We illustrate that our study can provide a novel unified framework for a joint computational and statistical asymptotic analysis on dynamic behaviors of these algorithms with the time (or the number of iterations in the algorithms) and large sample behaviors of the statistical decision rules (like estimators and classifiers) that the algorithms are applied to compute, where the statistical decision rules are the limits of the random sequences generated from these iterative algorithms as the number of iterations goes to infinity.