Victor Luo
SGD Distributional Dynamics of Three Layer Neural Networks
Dec 30, 2020
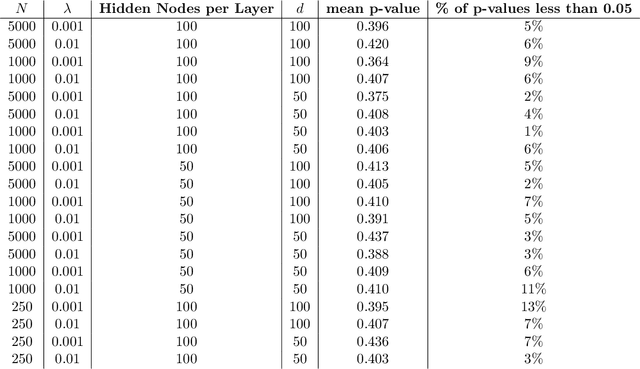


Abstract:With the rise of big data analytics, multi-layer neural networks have surfaced as one of the most powerful machine learning methods. However, their theoretical mathematical properties are still not fully understood. Training a neural network requires optimizing a non-convex objective function, typically done using stochastic gradient descent (SGD). In this paper, we seek to extend the mean field results of Mei et al. (2018) from two-layer neural networks with one hidden layer to three-layer neural networks with two hidden layers. We will show that the SGD dynamics is captured by a set of non-linear partial differential equations, and prove that the distributions of weights in the two hidden layers are independent. We will also detail exploratory work done based on simulation and real-world data.
How Many Factors Influence Minima in SGD?
Sep 24, 2020



Abstract:Stochastic gradient descent (SGD) is often applied to train Deep Neural Networks (DNNs), and research efforts have been devoted to investigate the convergent dynamics of SGD and minima found by SGD. The influencing factors identified in the literature include learning rate, batch size, Hessian, and gradient covariance, and stochastic differential equations are used to model SGD and establish the relationships among these factors for characterizing minima found by SGD. It has been found that the ratio of batch size to learning rate is a main factor in highlighting the underlying SGD dynamics; however, the influence of other important factors such as the Hessian and gradient covariance is not entirely agreed upon. This paper describes the factors and relationships in the recent literature and presents numerical findings on the relationships. In particular, it confirms the four-factor and general relationship results obtained in Wang (2019), while the three-factor and associated relationship results found in Jastrz\c{e}bski et al. (2018) may not hold beyond the considered special case.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge