From Random Search to Bandit Learning in Metric Measure Spaces

Random Search is one of the most widely-used method for Hyperparameter Optimization, and is critical to the success of deep learning models. Despite its astonishing performance, little non-heuristic theory has been developed to describe the underlying working mechanism. This paper gives a theoretical accounting of Random Search. We introduce the concept of \emph{scattering dimension} that describes the landscape of the underlying function, and quantifies the performance of random search. We show that, when the environment is noise-free, the output of random search converges to the optimal value in probability at rate $ \widetilde{\mathcal{O}} \left( \left( \frac{1}{T} \right)^{ \frac{1}{d_s} } \right) $, where $ d_s \ge 0 $ is the scattering dimension of the underlying function. When the observed function values are corrupted by bounded $iid$ noise, the output of random search converges to the optimal value in probability at rate $ \widetilde{\mathcal{O}} \left( \left( \frac{1}{T} \right)^{ \frac{1}{d_s + 1} } \right) $. In addition, based on the principles of random search, we introduce an algorithm, called BLiN-MOS, for Lipschitz bandits in doubling metric spaces that are also endowed with a Borel measure, and show that BLiN-MOS achieves a regret rate of order $ \widetilde{\mathcal{O}} \left( T^{ \frac{d_z}{d_z + 1} } \right) $, where $d_z$ is the zooming dimension of the problem instance. Our results show that under certain conditions, the known information-theoretical lower bounds for Lipschitz bandits $\Omega \left( T^{\frac{d_z+1}{d_z+2}} \right)$ can be improved.

A Lipschitz Bandits Approach for Continuous Hyperparameter Optimization

One of the most critical problems in machine learning is HyperParameter Optimization (HPO), since choice of hyperparameters has a significant impact on final model performance. Although there are many HPO algorithms, they either have no theoretical guarantees or require strong assumptions. To this end, we introduce BLiE -- a Lipschitz-bandit-based algorithm for HPO that only assumes Lipschitz continuity of the objective function. BLiE exploits the landscape of the objective function to adaptively search over the hyperparameter space. Theoretically, we show that $(i)$ BLiE finds an $\epsilon$-optimal hyperparameter with $O \left( \frac{1}{\epsilon} \right)^{d_z + \beta}$ total budgets, where $d_z$ and $\beta$ are problem intrinsic; $(ii)$ BLiE is highly parallelizable. Empirically, we demonstrate that BLiE outperforms the state-of-the-art HPO algorithms on benchmark tasks. We also apply BLiE to search for noise schedule of diffusion models. Comparison with the default schedule shows that BLiE schedule greatly improves the sampling speed.

Stochastic Zeroth Order Gradient and Hessian Estimators: Variance Reduction and Refined Bias Bounds

We study stochastic zeroth order gradient and Hessian estimators for real-valued functions in $\mathbb{R}^n$. We show that, via taking finite difference along random orthogonal directions, the variance of the stochastic finite difference estimators can be significantly reduced. In particular, we design estimators for smooth functions such that, if one uses $ \Theta \left( k \right) $ random directions sampled from the Stiefel's manifold $ \text{St} (n,k) $ and finite-difference granularity $\delta$, the variance of the gradient estimator is bounded by $ \mathcal{O} \left( \left( \frac{n}{k} - 1 \right) + \left( \frac{n^2}{k} - n \right) \delta^2 + \frac{ n^2 \delta^4 }{ k } \right) $, and the variance of the Hessian estimator is bounded by $\mathcal{O} \left( \left( \frac{n^2}{k^2} - 1 \right) + \left( \frac{n^4}{k^2} - n^2 \right) \delta^2 + \frac{n^4 \delta^4 }{k^2} \right) $. When $k = n$, the variances become negligibly small. In addition, we provide improved bias bounds for the estimators. The bias of both gradient and Hessian estimators for smooth function $f$ is of order $\mathcal{O} \left( \delta^2 \Gamma \right)$, where $\delta$ is the finite-difference granularity, and $ \Gamma $ depends on high order derivatives of $f$. Our results are evidenced by empirical observations.

A More Stable Accelerated Gradient Method Inspired by Continuous-Time Perspective

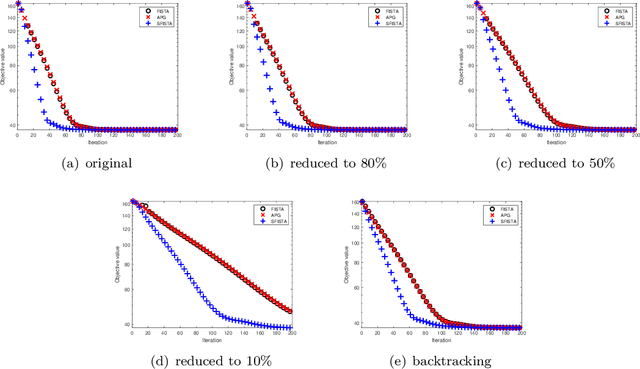
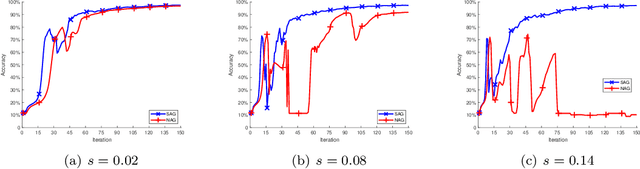
Nesterov's accelerated gradient method (NAG) is widely used in problems with machine learning background including deep learning, and is corresponding to a continuous-time differential equation. From this connection, the property of the differential equation and its numerical approximation can be investigated to improve the accelerated gradient method. In this work we present a new improvement of NAG in terms of stability inspired by numerical analysis. We give the precise order of NAG as a numerical approximation of its continuous-time limit and then present a new method with higher order. We show theoretically that our new method is more stable than NAG for large step size. Experiments of matrix completion and handwriting digit recognition demonstrate that the stability of our new method is better. Furthermore, better stability leads to higher computational speed in experiments.

Batched Lipschitz Bandits

In this paper, we study the batched Lipschitz bandit problem, where the expected reward is Lipschitz and the reward observations are collected in batches. We introduce a novel landscape-aware algorithm, called Batched Lipschitz Narrowing (BLiN), that naturally fits into the batched feedback setting. In particular, we show that for a $T$-step problem with Lipschitz reward of zooming dimension $d_z$, our algorithm achieves theoretically optimal regret rate of $ \widetilde{\mathcal{O}} \left( T^{\frac{d_z + 1}{d_z + 2}} \right) $ using only $ \mathcal{O} \left( \frac{\log T}{d_z} \right) $ batches. For the lower bound, we show that in an environment with $B$-batches, for any policy $\pi$, there exists a problem instance such that the expected regret is lower bounded by $ \widetilde{\Omega} \left(R_z(T)^\frac{1}{1-\left(\frac{1}{d+2}\right)^B}\right) $, where $R_z (T)$ is the regret lower bound for vanilla Lipschitz bandits that depends on the zooming dimension $d_z$, and $d$ is the dimension of the arm space.